1. 以太坊的数据组织
  2. 初步理解以太坊虚拟机
  3. EVM的设计与原理

这篇文章主要介绍以太坊的数据组织形式，构建以太坊各部分数据结构是如何组织的系统观。随后，我将会选取黄皮书中的核心设计思想，写得相对通俗易懂。各部分具体的数据结构，将会在后续的源码解读中给出。

概览

以太坊的区块由区块头和区块体构成，区块头存储元数据，通过区块哈希形成链式结构。区块体用于存储交易的集合和其他数据，大致结构如下：

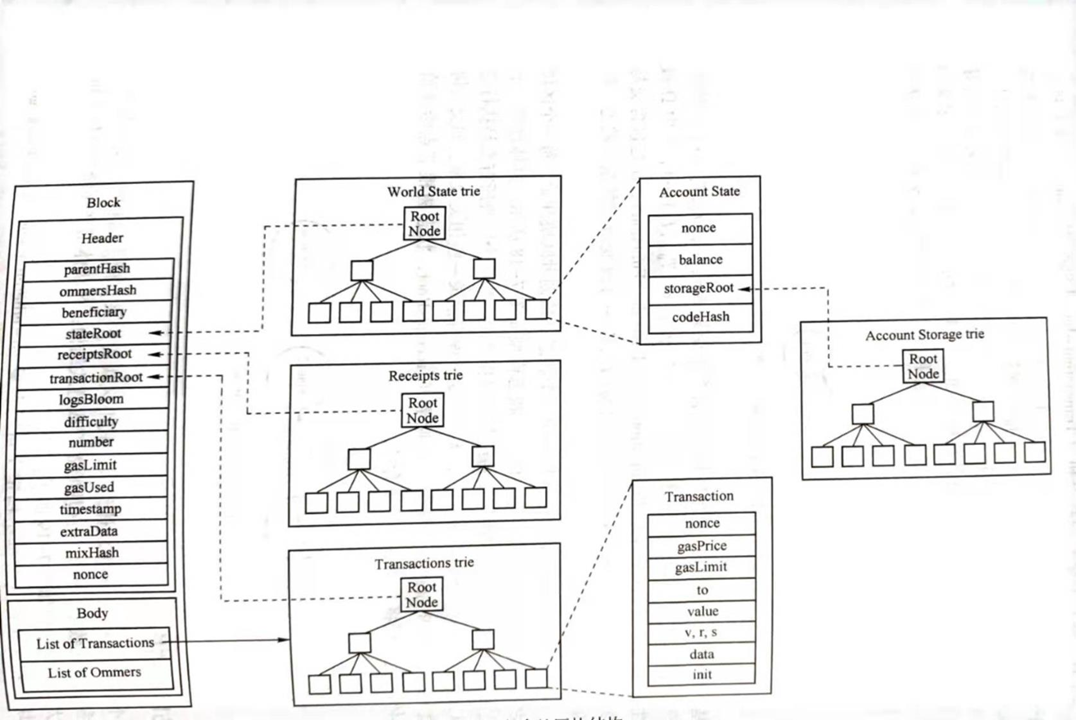
image-20220112232030495

Trie Tree

Trie Tree 被称作字典树，或者 前缀树 (prefix Tree)，用于管理键值对类型的多叉树。字典树的 Key 不是直接保存在某一个节点，而是通过节点在树中的位置确定，类似于哈夫曼编码树。因此，可知子节点都有相同的前缀。只有叶子节点才存放 Value，从根节点到叶子节点形成的路径上的节点，按照顺序排列构成 Value 的 Key.

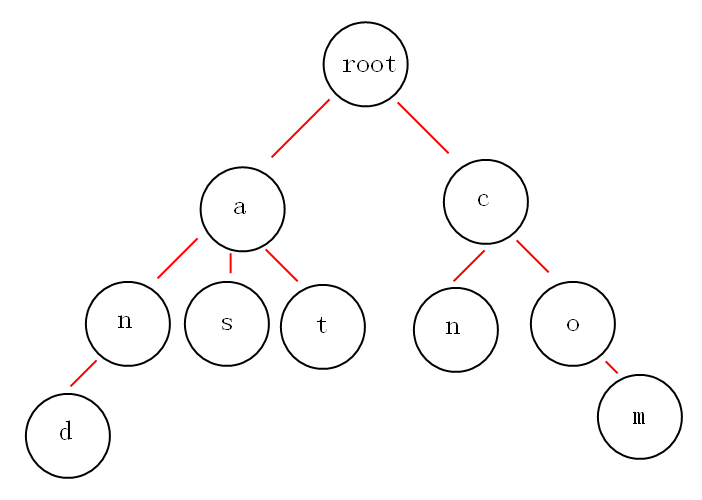
834896-20160614172111323-163074258

假如 节点 d 存储 Value，则 and 是它的 Key

总体如下：

  • 根节点不包含字符，根节点外的所有节点都只包含一个字符。
  • 从根节点到某个节点，路径上经过的的字符连起来，为该节点对应的 Key.
  • 每个节点的 Key 互不相同。

可知 Trie Tree 用空间换时间，但是 Key 的差异性很大时，构成的树可能会很不“整齐”，就像二叉排序树一样需要平衡。例如下面的情况：

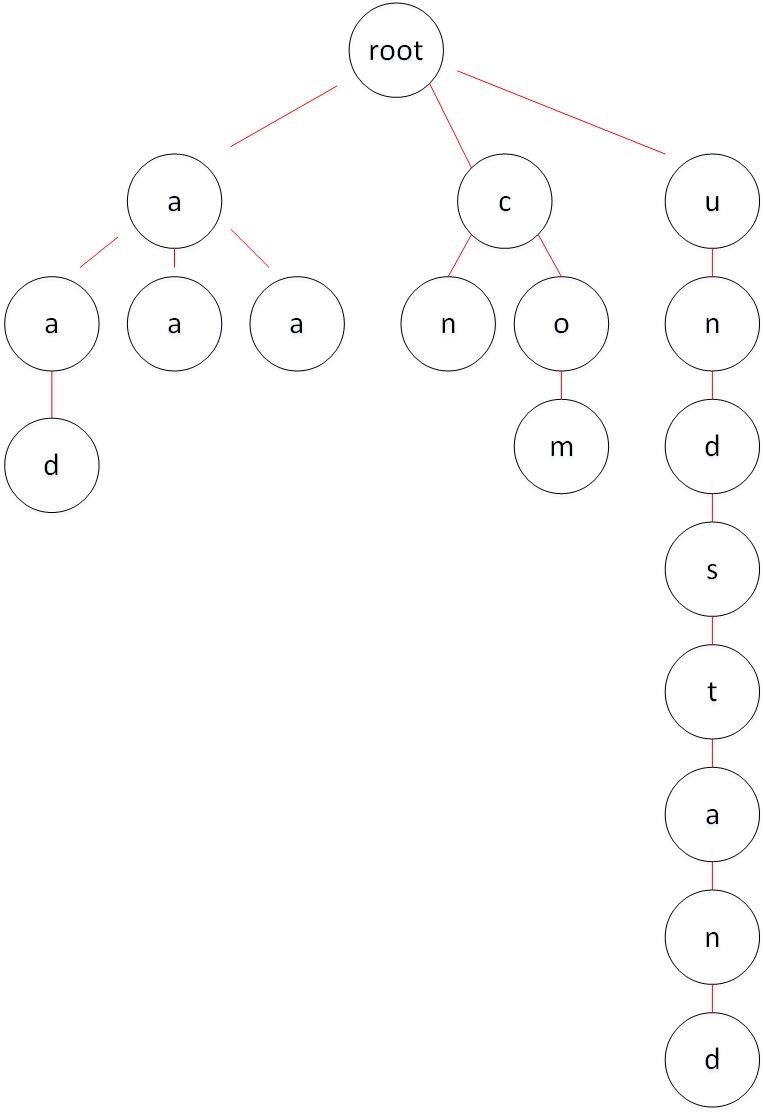
834896-20160614172159901-1784091467

Patrica Tree

Patrica Tree 被称作 Compact Prefix Tree，是一种存储空间优化的字典树。Patricia Tree 的非叶子节点至少有两个子节点，这样就可以让树更加“均衡”。

MPT

MPT 融合了 Merkle Tree 和 Patricia Trie 的优势，其中 Merkle Trie 用于完整性校验，Patricia Trie 用于优化 Trie Tree。在以太坊中，MPT 用于组织账户状态集合、交易数据集合、合约状态集合等数据结构，非常的重要。在一般的 MPT 的基础上，以太坊采用哈希只作为节点的值，并且采用 4 种节点类型，压缩树的的高度，使它更 “平衡”，降低了复杂度。

  • 空节点。表示空串。
  • 叶子节点。表示键值对，Key 是十六进制前缀编码（Hex-Prefix, HP），Value 是数据的 RLP 编码（Recursive Length Prefix）。
  • 拓展节点。也表示键值对，用于存储公共前缀的数据。拓展节点可以拓展出一个分支节点。
  • 分支节点。键值对。表示 MPT 中所有拥有超过一个子节点的非叶子节点。Key 是长度为 16 的数组，数组的下标用 0-F 的十六进制数表示，数组的值是分支节点的哈希值。第十七个元素存储 Value 。

HP 编码

HP 编码用于区分拓展节点和叶子节点，在 Key 前增加一个字节编码，来表示 Key 对应的值是 Value 还是分支节点的哈希值。

编码操作：

  • 如果 Key 末尾字节表示的十六进制数是 F, 则表示是叶子节点，需要将末尾的这个字节去除。然后在 Key 的开头增加一个字节，这 8 位分成两部分，高四位用于编码节点类型，第四位编码 Key 长度的奇偶性。

RLP 编码

RLP 编码是以太坊数据序列化和反序列化的主要方法。区块、交易、账户等数据都会先经过 RLP 编码，再持久化存储再数据库中。数据序列化类似于将数据转化成 JSON 格式，反序列化相当于把 JSON 格式转换成原格式。RLP 不定义任何特定的数据类型，而是数组嵌套的方式存储结构化的数据。RLP 中的数据类型只有两种：

  • 字符串。用二进制序列表示。
  • 列表：递归嵌套的结构，类似于 Python 中的列表。

其他类型需要编码时转化成上面的两种类型之一，转化规则可以自定义。

注：这一段所有数字默认十六进制，特殊的会额外说明。

注：定义列表长度为列表第一层项数加上每一项元素的长度。如果元素也是列表，则按定义递归。

编码规则：

输入类型 编码方法
单个字节 字节本身 ASCII 码作为编码内容。
单个字符串且 ASCII 解码后不大于 55（十进制）个 字节 在字符串的 ASCII 码前加上前缀（0x80+字符串字节数）
如："abc"的 ASCII 编码是 “61 62 63”，3 个字节，因此前缀为 80+3=83，编码后 “83 61 62 63”（注意均十六进制）
单个字符串且 ASCII 解码后大于 55（十进制） 个字节 在字符串的 ASCII 码前加上两个前缀（0xb7+字符串字节数存储时的字节数）和字符串字节数。
列表且长度不大于 55（十进制） 在列表元素的编码前加上前缀（0xc0+列表长度），
列表且长度大于 55（十进制） 在列表元素的编码前加上两个前缀，（0xf7+列表长度存储时的字节数)和列表长度。

第二种类型的例子：

如：“abc” 数以第二种类型，它的 ASCII 编码是 “61 62 63”，3 个字节，因此前缀为 80+3=83，编码后 “83 61 62 63”（注意均十六进制）

第三种类型的例子：

如：“Lorem ipsum dolor sit amet, consectetur adipisicing elitLorem ipsum dolor sit amet, consectetur adipisicing elit” 属于第三种类型，编码成十六进制为 4c6f72656d20697073756d20646f6c6f722073697420616d65742c20636f6e7365637465747572206164697069736963696e6720656c69744c6f72656d20697073756d20646f6c6f722073697420616d65742c20636f6e7365637465747572206164697069736963696e6720656c6974，共 112（十进制）个字节，需要 1 个字节存储 112（十进制）。因此，第一个前缀为 (67+1)=68，第二个前缀为 38。因此，最终编码为68384c6f72656d20697073756d20646f6c6f722073697420616d65742c20636f6e7365637465747572206164697069736963696e6720656c69744c6f72656d20697073756d20646f6c6f722073697420616d65742c20636f6e7365637465747572206164697069736963696e6720656c6974。计算程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func rule3(string2 string) {
	text := []byte(string2)
	hexSeq := hex.EncodeToString(text)
	bytesOfLen := len(text)
	bytesNeedOfLen := 0
	for bytesOfLen != 0 {
		bytesNeedOfLen++
		bytesOfLen /= 2
	}
	bytesNeedOfLen = int(math.Ceil(float64(bytesNeedOfLen) / 8))
	prefix1 := fmt.Sprintf("%x", bytesNeedOfLen+0x67)
	prefix2 := fmt.Sprintf("%x", int(math.Ceil(float64(len(text)/2))))
	fmt.Printf("%v\n%v\n%v", prefix1+prefix2+hexSeq, prefix1, prefix2)
}

后面几种类型有些复杂，理解思想即可。

状态树

每个区块都有一个状态树，账户模型的集合作为叶子，然后根据全局的 MPT 生成代表这个区块全局状态的 stateRoot，

收据树

区块链的收据是一种“轻量级”的对数据存在性的证明。假如收据的存在，则说明它对应的收据已经被区块链验证过了。

参考：