(七)抽象解释
前言
这一文章是理论课,对之前的程序分析的合理性和思路,进行了理论上的分析和论证,有助于读者培养程序分析的思维。程序分析的很多思路都是对具体的值具体的表达式进行了抽象,建立了具体空间和抽象空间的关系,抽象解释理论就是解释映射函数。
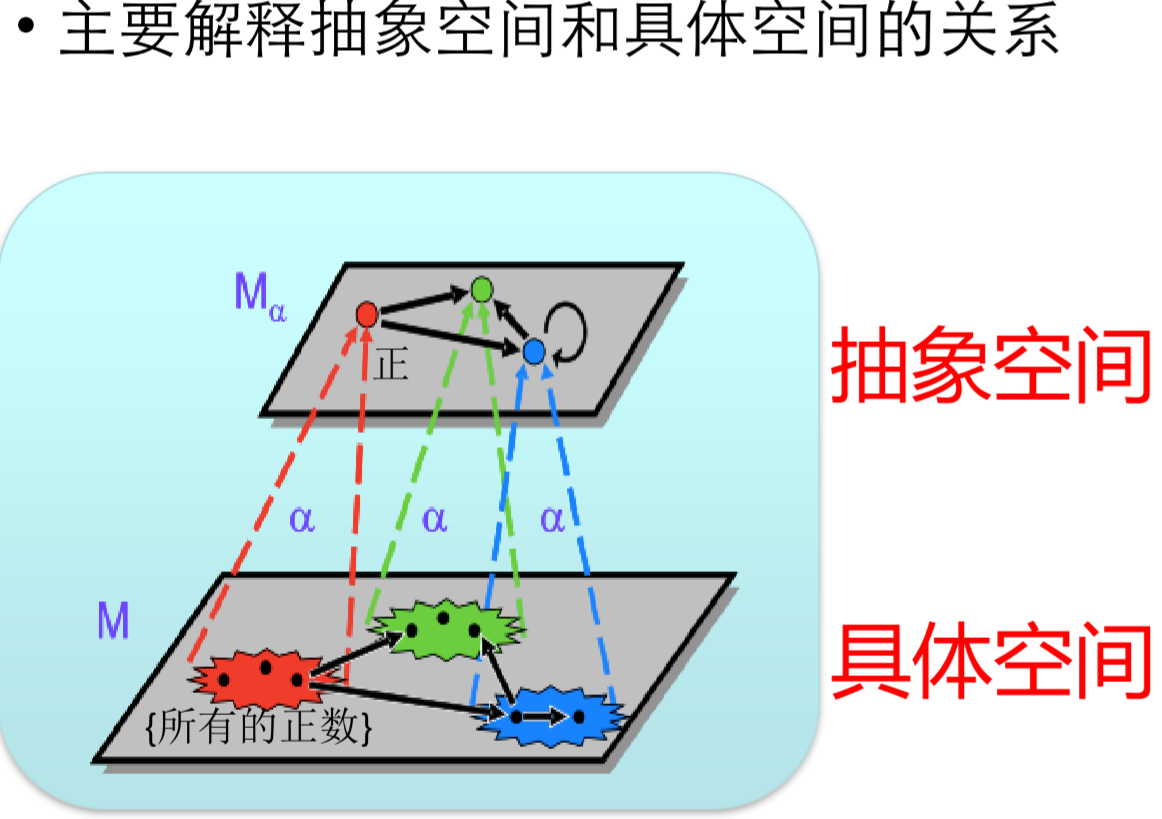
这个映射主要分成两部分:
- 具体化函数 将抽象值映射为具体值的集合
- 抽象化函数 将具体值的集合映射为抽象值
伽罗瓦连接 Galois Connection
假设抽象域上存在偏序关系。简便起见,这里假设具体值集合上的偏序关系为子集关系。但抽象解释理论支持其他偏序关系,比如超集。
注意下面特殊的字 虚 表示抽象域集合,甲 表示抽象域集合中的元素。任取两个集合中各自一个元素 X 和 甲,那么如果满足如下的条件,就构成了伽罗瓦连接。

除了上面的定义意外,还有更加详细的定义,他们可以更加容易的看出映射函数的性质。为了加快学习速度,我不详细说明证明过程了。这让我想起来《信息安全数学基础》,学了一堆近世代数的东西,可能我当时不知道有什么特别的用途吧,但是认真学习下来确实锻炼了抽象化的能力,去考虑性质和映射。

抽象域的安全性
我们探讨,抽象域上的操作,是否对于具体域是安全的,也就是说,不会包含预料外的结果。安全性 其实一个比较灵活的词,根据不同的分析会有不同的含义,比如指针分析是 may 分析,允许有超出实际指向的情况的结果,它的安全性就是包括了所有可能指向的对象。但是对于编译器优化来说,它为了保证语义,它的安全性是,一定不会改变语义才是安全的,也就是 must 分析。
可以证明,一定可以找到合适的变化的函数。

老师还以数据流分析的安全性为例,作了说明,后面还说明了路径的安全性。但是我暂时跳过了。感兴趣的读者可以见视频。
常见抽象域
关系抽象
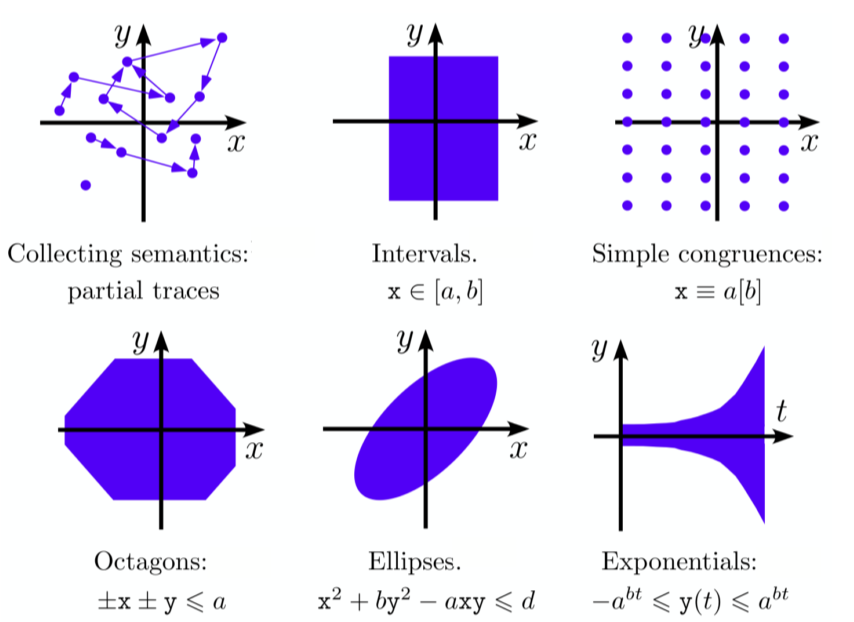
考虑变量之间的关系映射到抽象域上,这里以数值计算为例。老师举了一个比较巧妙地例子「八边形抽象」,用于理解关系抽象的约束,可以更加精确地分析。视频讲的很清楚不赘述了。
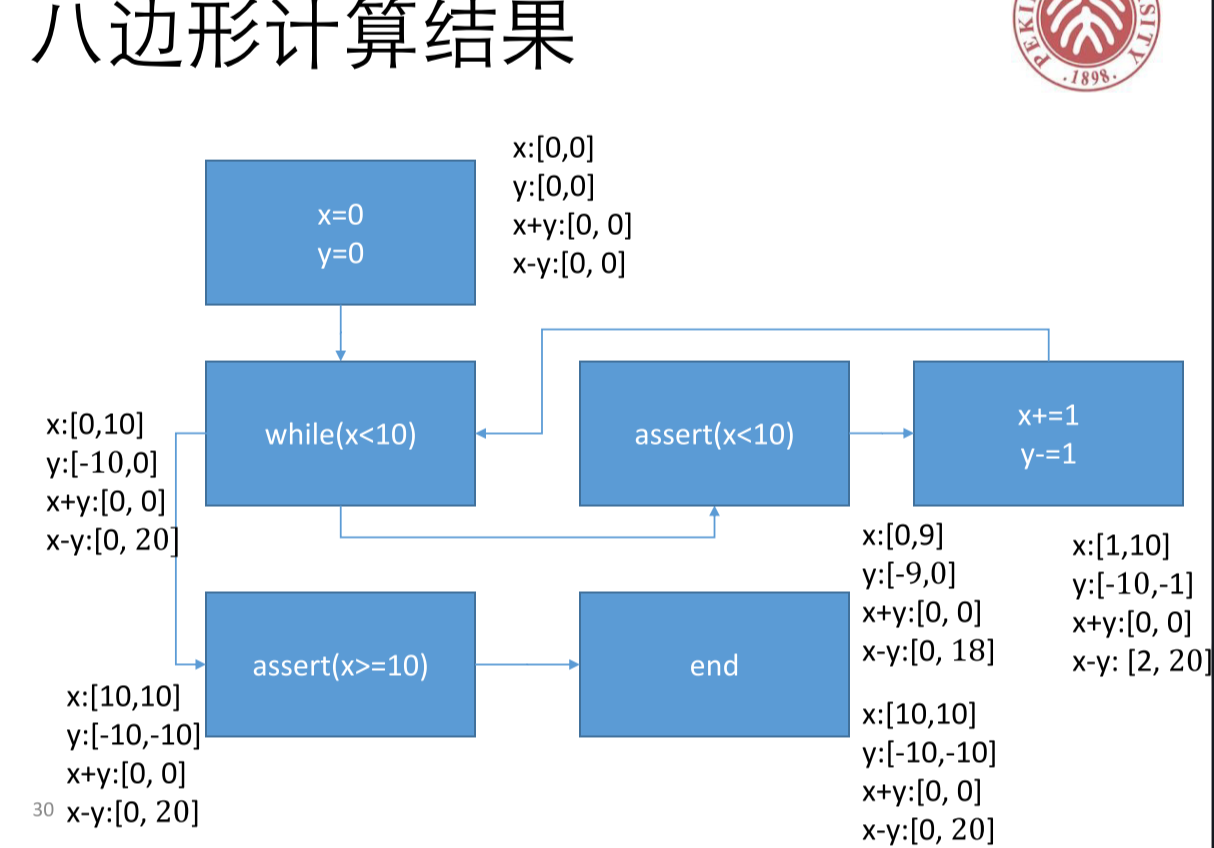
下面是一个区间分析,虽然我也不记得 narrowing 和 widening 的具体规则了,但是可以感受到,添加了 x+y x-y 这样的约束,可以更加精确地表示出 x y 的范围。
其他的数值抽象还有各种各样的图形,下面是比较简单的用平面图形就可以表示的情况,实际上高维的情况也是成立的,所以关系抽象是非常复杂但是应该也比较实用。
谓词抽象
这个比较容易理解,把一堆属性,用谓词产生对应的真值序列或者矩阵。比如 x>0,x=0,x<0 就可以抽象成 [true,false,false] 之类的。
体验抽象解释工具
最后,可以玩一玩这个抽象解释工具,这是一个用于教育意义的 demo。他自己设置了一个简单的语言,比如它给的例子
1 | proc incr (x:int) returns (y:int) |
矩形抽象域(box)下的结果,可以知道 incr 里面 x 的范围,接着就知道了 y 的范围,进而就知道了返回值 i 的范围。
1 | proc incr (x : int) returns (y : int) var ; |
八边形抽象域(octagon),可以得到 的形式的约束,具体生成过程就不细究了。
1 | proc incr (x : int) returns (y : int) var ; |



