（一）初识软件分析

1. （一）初识软件分析
2. （二）数据流分析基础
3. （三）Datalog和程序分析
4. （四）静态单赋值和稀疏分析
5. （五）过程间分析
6. （六）指向分析
7. （七）抽象解释
8. （八）SMT和符号执行
9. （九）体验静态分析工具
10. （十）Fuzzing 基础

这篇文章，或者说软件分析这一个系列更像是学习笔记，绝大部分内容来自于“北大-熊英飞-软件分析”，以及南大的静态分析课程，感谢他们提供高质量的公开课，课程资源将会在文末给出。除了老师们的公开课，文章中可能会包括我自己的总结以及从其他学习资料（如博客、书等）中的内容，补充完善这篇文章。

为什么学习智能合约安全需要学习软件分析呢？因为，合约的代码安全非常重要，而代码的分析，乃至代码编译成的字节码的分析，可以笼统的归纳为软件工程的内容。当合约审计人员熟悉了合约审计工具的使用，能够避免目前已经被发现的漏洞时，如果还希望再进一步，从 DApp 开发人员变成区块链安全负责人，软件分析是绕不开的技能。从熟悉各种业务场景的合约漏洞，到学会使用审计工具辅助审计，到弄懂审计工具原理后自己编写合约审计工具，到区块链平台上合约漏洞检测和攻击检测，软件分析的知识将会是“成功的第一步”。

学习完基本的知识后，我们将会进入智能合约分析方法（包括形式化验证、fuzzing、程序分析、机器学习、污点分析等）的学习。

最主要的参考资料如下，读者如果有不理解的地方，可以找到对应内容学习：

• 北大 熊英飞 软件分析公开课主页和视频。
• 沉浸式《程序分析》教材。
• 南大 Static Program Analysis 和对应视频。
• https://www.cs.cmu.edu/~aldrich/courses/17-355-19sp/
• https://cs.au.dk/~amoeller/spa/spa.pdf

程序分析概览

此部分（程序分析概览）大部分来自「沉浸式《程序分析》教材」，感谢南大的老师这篇引人入胜的入门级文章。

程序分析是指：在不运行一个程序的情况下，通过某种方法分析该程序就知道其是否满足某些性质。这种“不运行程序”的状态也称为**“静态”或“编译时（compile-time）”**（它们分别与程序的“动态”和“运行时（run-time）”相对应），这种分析方法也被叫作程序分析、静态程序分析或静态分析。

程序分析的用途概览：

• **程序可靠性（Program Reliability）**想必你应该经历过程序崩溃后报错信息中显示的空指针异常吧，是的，像这种影响程序可靠性的诸多 bug，很多都可以被程序分析在静态时检测出来，包括那些可能会导致程序不响应的程序缺陷，如内存泄漏。

• **程序安全性（Program Security）**程序分析几乎是软件安全必学的内容之一。

• **编译优化（Compiler Optimization）**源码中的许多操作在编译时可以转换成更加高效的方式。此外，dead code elimination 可以避免永远执行不到的代码编译进程序； code motion 可以将某些表达式移动到其他位置，减少重复计算的冗余。

• **程序理解（Program Understanding）**程序理解和 IDE 设计非常相关，例如调用关系、继承关系、声明类型等信息都需要通过程序分析的方法获取。程序的调试有时也需要程序分析技术的辅助。

程序设计语言：

程序分析属于程序设计语言的一部分，程序设计语言可以主要分成三类研究内容：

• 理论。设计程序设计语言一般是从其语法、语义的设计开始，也包括选择什么类型系统，支持什么语言特性等问题。一般情况下，这类理论研究一般可以自证，即我可以将语言的语法、语义、类型系统等形式化，然后在其形式化基础上用理论方法证明该语言的诸多性质，这也就是为什么很多 PL 的论文并没有实现实验部分。
• 环境。程序设计语言有了理论设计，在实际中想要运行的起来，必须要有支撑它的环境系统，这主要包括编译系统和运行时系统两个部分，编译系统强调语法的解析（如果是静态语言还会有类型检查等），运行时系统强调语义的解释执行（比解释器更复杂的运行时系统也会负责垃圾回收等内存问题）。PL 的环境系统往往避免不了在实现细节上做很多脏活累活，使得语言在实际中真能好用起来。
• 应用。有了理论与环境的支撑，语言就能跑起来了，然而，一个工业级的程序设计语言通常是一个非常复杂的系统，如何保障该复杂系统的可靠性、安全性、高性能等需求，是需要一系列方法来支撑的，这些方法（如程序分析、程序验证、程序合成等）通常要以语言的理论部分为基础（如语法、语义），结合不同的数学理论来完成各自应用的目标。在 PL 应用中，最具代表性的技术就是程序分析。

程序设计语言虽然数量繁多，但也无非属于以下三大类（我们通常称之为程序设计语言范式，Programming Paradigm），它们分别是：

• 命令式程序设计语言（Imperative programming languages，IP）
• 函数式程序设计语言（Functional programming languages，FP）
• 逻辑式程序设计语言（Logic programming languages，LP）

它们详细地介绍：

• 在 IP 中，指令一个一个给出，用条件、循环等来控制逻辑（指令执行的顺序），同时这些逻辑通过程序变量不断修改程序状态，最终计算出结果。我觉得，尽管 IP 现在都是高级语言了，但是本质上并没有脱离那种“类似汇编的，通过读取、写入等指令操作内存数据”的编程方式（我后面会提及，这是源于图灵机以及后续冯诺依曼体系结构一脉的历史选择）。国内高等教育中接触的绝大多数编程语言都是 IP 的，比如 Java、C、C++等。
• 在 FP 中，逻辑（用函数来表达）可以像数据一样抽象起来，复杂的逻辑（高阶函数）可以通过操纵（传递、调用、返回）简单的逻辑（低阶函数）和数据来表达，没有了时序与状态，隐藏了计算的很多细节。不同的逻辑因为没有被时序和状态耦合在一起，程序本身模块化更强，也更利于不同逻辑被并行的处理，同时避免因并行或并发处理可能带来的程序故障隐患，这也说明了为什么 FP 语言如 Haskell 在金融等领域（高并发且需要避免程序并发错误）受到瞩目。
• LP 抽象的能力就更强了，计算细节干脆不见了。把你想表达的逻辑直观表达出来就好了。 如今，在数据驱动计算日益增加的背景下，LP 中的声明式语言（Declarative programming language，如 Datalog）作为代表开始崭露头角，在诸多专家领域开拓应用市场。

理解不完备性

哥德尔不完备性定理

哥德尔不完备性定理指出：『包含自然数和基本算术运算（如四则运算）的一致系统一定不完备，即包含一个无法证明的定理。』其中，完备性指所有真命题都可以被证明。一致性指一个定理要么为真要么为假。

这表面，程序的运行结果是不确定的，对于初学者，在直觉上可能难以接收。下面给说明：

我们假定命题 A: 不存在其他命题 x 可以确定 A 为真。那么就有两种情况。

1. 如果 A 为假，那么就存在 x 可以使得 A 为真，矛盾。
2. 如果 A 为真，那么说明 A 为真是无法推导出来的。而我们却假定了 A 为真，这说明 命题 A 的真假可能存在，但是我们无法判断 A 是真还是假。

图灵：停机问题

类似的，对于停机问题，图灵证明：不存在一个算法能回答停机问题。我们可以假设存在一个算法 B 可以判断停机问题（任何情况下可以知道任何输入下是否会停机），即命题 B：对于给定程序 x，x 会停机。那么我们在程序 x 中包含命题 B，让 B 为真时程序 x 不停机，这会造成：

• 如果为真，则 Evil 不停机，矛盾
• 如果为假，则 Evil 停机，矛盾

不可判定

接下来，定义可判定问题：对于回答是或否的问题，如果存在一个算法，使得对于该问题的每一个实例都能给出是/否的答案，那么就是可判定问题。回到程序中，我们可以知道以下问题是不可判定的：

• 给定程序和输入，判断程序是否会抛出异常。
• 给定无循环和函数调用的程序和特定输入，判断程序 是否会抛出异常。

莱斯定理

将任意程序看作是从输入到输出的函数，或者将程序看作是包含输入到输出的所有映射的集合，那么莱斯定理证明了：『关于该函数/集合的任何非平凡属性，都不存在可以检查该属性的通用算法』

其中：

• 平凡属性：要么对全体程序都为真，要么对全体程序都为假。

也就是说，我们无法通过通用的方法，判断所有程序是否有某个性质。

不完备性中的确定性

模型检查

如果学习过状态机的话，我们可以知道对于

• 状态的数量是有穷的。
• 对于每个状态，它将转移到的下一个状态是确定的。
• 将状态转移视作有向图，这个有向图不构成环。

的情况，这个状态机一定的终止，也就是说建立在状态机上的函数一定会终止。这说明『对于有限的情形，我们可以知道程序的运行情况』。但是，它将会消耗比需要检查的程序更多的计算资源。例如，某个程序计算整数的加法，如果我们遍历了

$$\forall 0\leqslant m<n<10^6 \\ A=\left\{ \sum_{i=m}^n{i} \right\}$$

那么，可以知道从 1 加到 10 的结果。但是，如果检查一个程序的所有状态所需要的资源变得无穷大（例如调用自身造成死循环），那么这个程序的结果是无法判定的。

这种基于有限状态机模型抽象判断程序属性的办法就叫做模型检查。它的缺点很明显，如果状态数量太多，将会造成状态爆炸，无法用于大型的程序。

近似方法

当得不到准确答案时，我们可以得到得到近似解，极大的减少工作量。近似的方法可以分成两种：

1. 只输出“是”或者“不知道”，这叫做 must analysis, lower/under approximation(下近似，因为这样得到的情况会是实际情况的子集)
2. 只输出“否”或者“不知道”，这叫做 may analysis, upper/over approximation(上近似，因为这样得到的情况会是实际情况的超集)

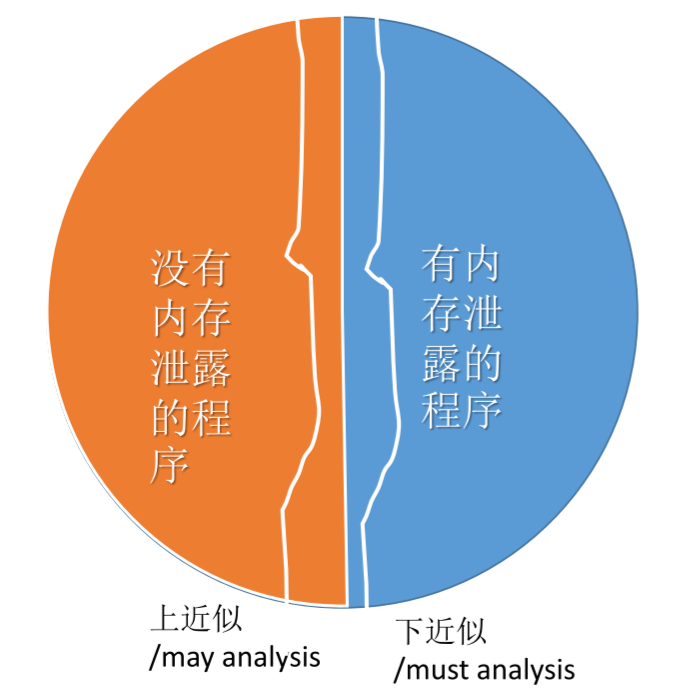
如果我们能够同时做到上近似和下近似，那么就称作满足完整性(completeness)；如果只是满足其中的一种，就称作满足健壮性、安全性或者正确性(soundness、safety、correctness)。

抽象

为了近似求解，比如我们判断变量 a == 5，那么可以退而求其次只尝试分析 a 是否是正数。一般的抽象方法将抽象出新的抽象集合和运算规则。

比较特殊的是，对于运算规则而言，输入和结果都不一定是确定的值，我们可以保留 “未知”。

搜索

搜索是指确定某种情况，例如变量 a==5，然后开始启发式的搜索（例如动态调整搜索路径、剪去不必要的“枝叶”），如果得到了 a==5，那么确定本次搜索成功，程序满足这个性质。否则，程序遍历完所有可能结果、搜索超时或者找到范例，那么本次搜索失败，不知道是否满足这个性质。

优化搜索方式是这种近似方法的关键。

编译基础

编译器（Compiler）是一种计算机程序，它会将用某种编程语言写成的源代码（原始语言），转换成另一种编程语言（目标语言）。

一般来说编译器的内部包含了如下的工作步骤：

1. 词法分析；
2. 语法分析；
3. 语义分析；
4. 生成中间表示（intermediate representation，IR）；
5. 代码生成；
6. 优化；

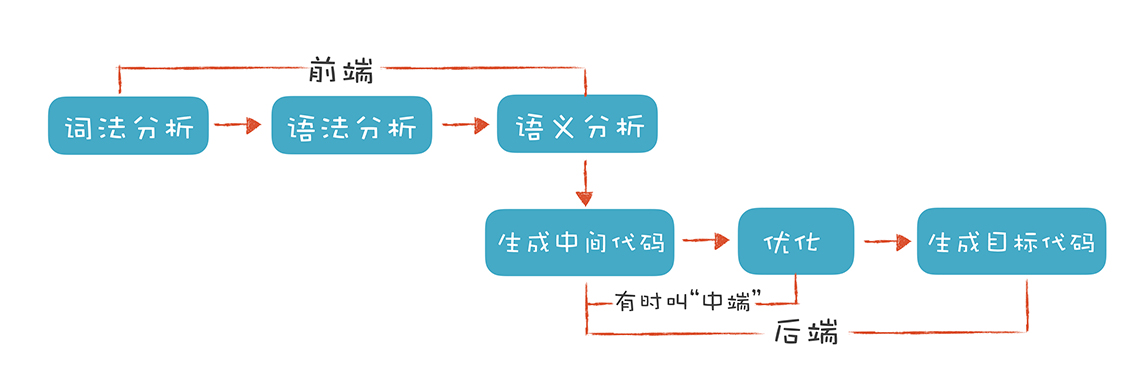
其中 1-4 步称作编译器的前端，4-6 步称作编译器的后端。

词法分析

词法分析的主要工作是将源代码的字符流转换成 Token 流，这一步通常是由词法分析生成器，根据给定的规则把输入构建成 Token。例如：

int a = 0;

对应的会生成 int，a，=，0，; 这几个 Token.

严格的说，token 包括 种别码 和 属性值，种别码可以分成如下类型：

详细的例子如下：

文法的形式化定义

文法是语言的规则，形式化定义如下

$$G=\left( V_T,V_N,P,S \right)$$

• $V_T$ 表示终结符集合，也就是文法字符集中的基本符号。
• $V_N$ 表非终结符集合，也就是非基本符号，一般是基本符号的组合。
• $P$ 表示产生式集合。描述了终结符号和非终结符号组合成串的方法。
• $S$ 表示开始符号。

产生式 $P$ 可以形成推导和归约两种推理逻辑，因为 $P$ 定义了 $$(V_T∪V_N)^+\rightarrow (V_T∪V_N)^*$$ 的规则，这可以简单的理解为从抽象到具体的推导。

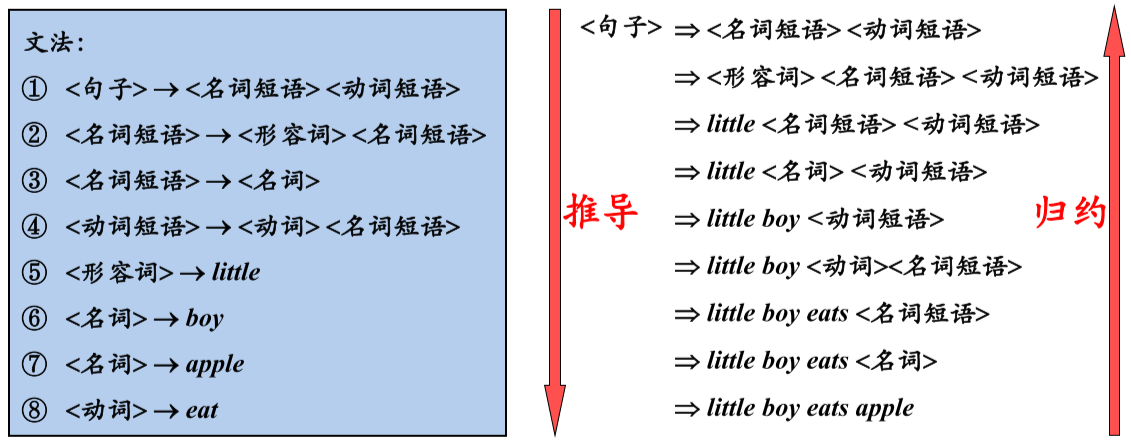
特别地，开始符号化经过若干步推导出词串被被称作句型，如果句型中全部都是终结符，也就是具体地值或者基本符号，那么就称作句子。

$$S\Rightarrow ^*\alpha$$

更进一步，如果遍历所有句子，那么就称作语言，记为

$$L(G)=\left\{ w\mid S\Rightarrow ^*w,w\in V_{T}^{*} \right\}$$

因此，如果需要判断某个词串是否是某个意思，只需要将具体的表达式归约到符号，判断它是否满足某个特定的文法规则。

下面根据流程进一步的解释

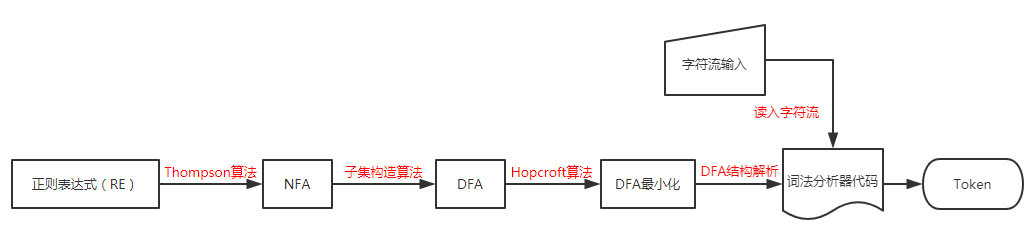
首先，将规则转化成状态机。Thompson 算法能将正则表达式转化为一个与之等价的非确定有限状态自动机（NFA 是对每个状态和输入符号对可以有多个可能的下一个状态的有限状态自动机），它可以巧妙地将语法规则由正则表达式转化 NFA，类似于下图

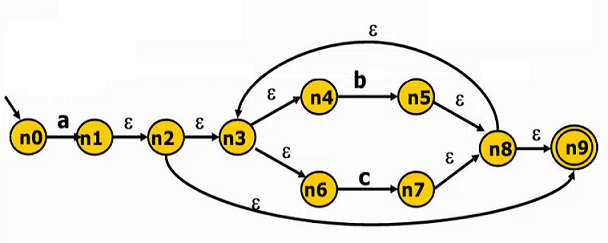
然后，根据子集构造算法将 NFA 转换成 DFA（有限状态机）。

接着，通过 Hopcroft 算法进行状态化简，如果读者学习过数字逻辑中的时序逻辑，应该不会陌生。这一步可以有效减少状态数，去除冗余的状态。

最后，在词法分析器中，DFA 进一步地解析，和读取地字符流一起生成 Token.

语法分析

语法分析（英语：syntactic analysis，也叫 parsing）是根据某种给定的形式文法对由单词序列（如英语单词序列）构成的输入文本进行分析并确定其语法结构的一种过程。

简单地说，词法分析类似于字母组成单词的过程，根据字符生成 Token。语法分析是把单词组合成语句，Token 会按特定的规则构成语法树。

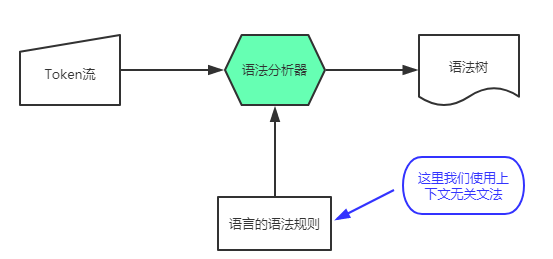
上下文无关法用于描述程序设计语言的语法，维基百科如此解释

上下文无关文法重要的原因在于它们拥有足够强的表达力来表示大多数程序设计语言的语法；实际上，几乎所有程序设计语言都是通过上下文无关文法来定义的。另一方面，上下文无关文法又足够简单，使得我们可以构造有效的分析算法来检验一个给定字符串是否是由某个上下文无关文法产生的。

语法分析器（parser）通常是作为编译器或解释器的组件出现的，它的作用是进行语法检查、并构建由输入的单词组成的数据结构（一般是语法分析树、抽象语法树等层次化的数据结构）

分析树树举例：

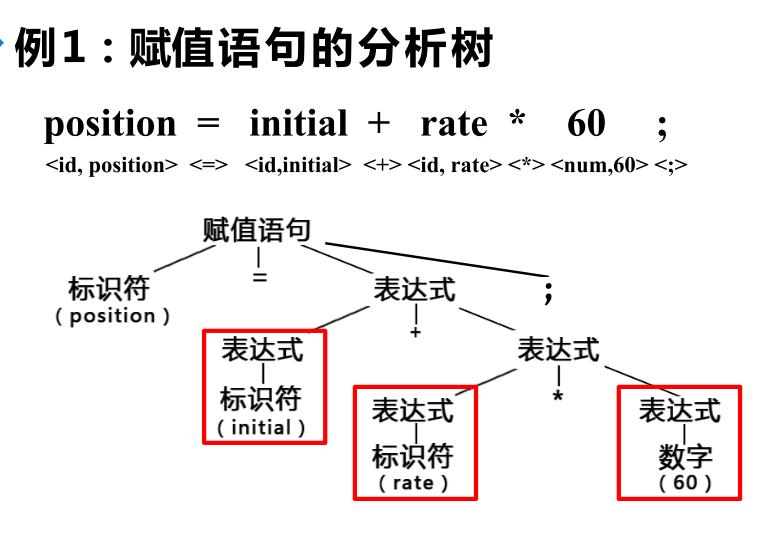
声明语句 -> 类型 标识符序列

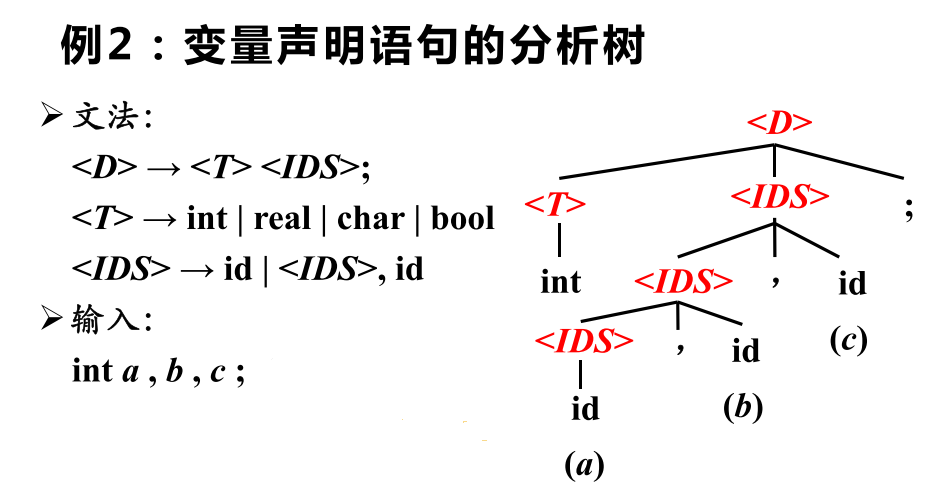
抽象语法树举例：

辗转相除法的语法树：

while b ≠ 0
if a > b
a := a − b
else
b := b − a
return a

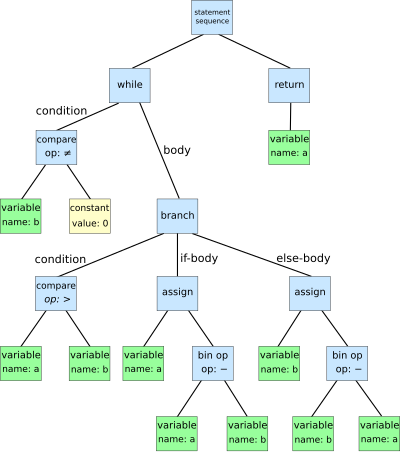
你也可以在这个在线网站中，直观的观察 AST.

语义分析

语义分析也称为类型检查、上下文相关分析。它负责收集和检查程序（抽象语法树）的上下文相关的属性。大致包括如下属性：

• 种属(kind)，如简单变量、复合变量、过程等
• 类型(type)
• 存储位置和长度
• 值
• 作用域
• 参数和返回值信息等

收集到的属性信息会存放在符号表中，它附属了一个字符串表，由每一行的标识符构成。这样只要记录标识符的起始位置和长度即可。

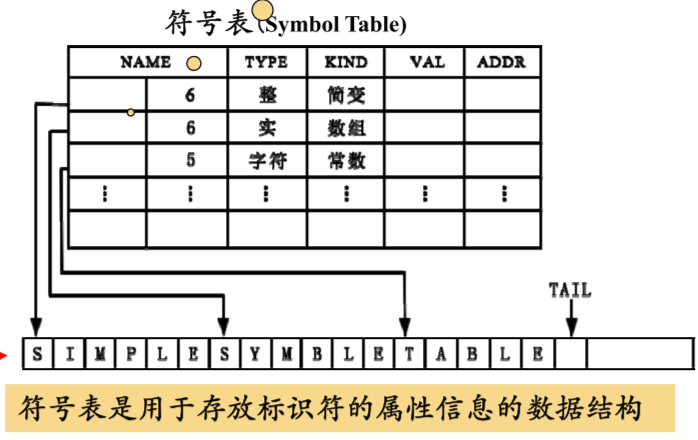
标识符语义往往和语言特性非常相关，检查的属性大致包括

• 变量在使用前先进行声明。
• 每个表达式都有合适的类型，推测类型。
• 函数调用和函数的定义一致。
• 操作符和操作数类型匹配。如数组下标必须是整数。
• 等等。

中间代码生成

常见的中间表示包括三地址码 (Three-address Code) 和语法结构树/语法树 (Syntax Trees)。

三地址码

三地址码和 mips 指令集架构类似，但是运算可以用更高级的方式表示。

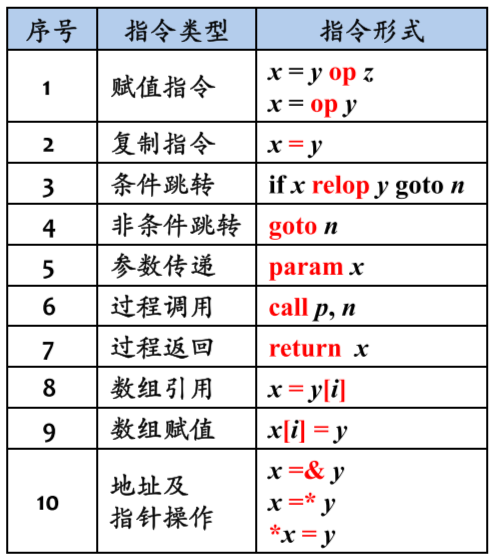
下面是一个例子，注意左边的是语法分析树而不是语法树，右边则是三地址码的四元表示，其中第四个位置表示赋值地址。

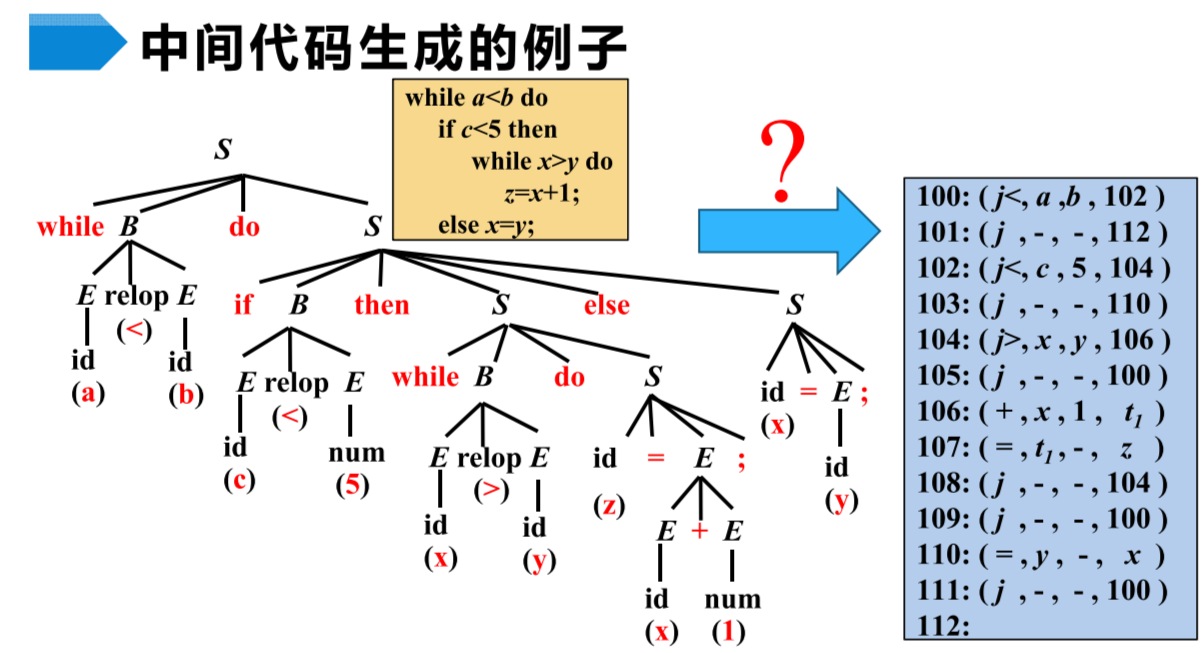
语法树

语法树是我们关注的重点，注意它和语法分析树(Parser Tree)不是一回事。

以 solidity 为例，编译器给出的结果可以通过如下方式得到：solc --ast-compact-json storage.sol，可以格式化 json 仔细观察。

代码生成

代码生成是把中间表示形式映射到目标语言，这样可以合理的分配到寄存器中。

其他参考资料

• 编译语言词法分析
• 聊聊编译原理（二） - 语法分析
• 汤普森构造法
• 上下文无关文法
• 编译原理之美笔记
• 编译原理 哈工大