(四)静态单赋值和稀疏分析
简介
这一章是对数据流分析的拓展和补充,基本内容如下:
首先从 Def-Use 的角度对控制流图进行简化,但是发现如果变量被多次赋值或者定义,那么简化操作反而会增加更多的边。因此,引入了静态单赋值的方法,所有变量都只赋值一遍,并且再次赋值则视作新的变量。但是分支交汇处的变量,将会不知道来自于其中哪一个分支,因此引入了交汇函数,将所有分支的变量交汇。但是哪些地方需要引入交汇操作呢?探讨了最直接的每个基本块都引入教会操作,但是引入了大量的冗余操作。进而学习了基于支配边界的确定交汇操作的方法。
Def-Use
提出问题
之前的数据流分析中,每个数据节点都必须保存所有的值(抽象域),这就导致即使这个数据节点没有对其中某个值,进行任何的读取或者其他操作,也必须分配额外的存储空间。另外,我们之前假设是所有的数据节点都是有关的,要么是正向分析,要么是逆向分析。但是实际上,可能只有少数几个节点之间的变量才会存在依赖关系。
一个例子见下图:
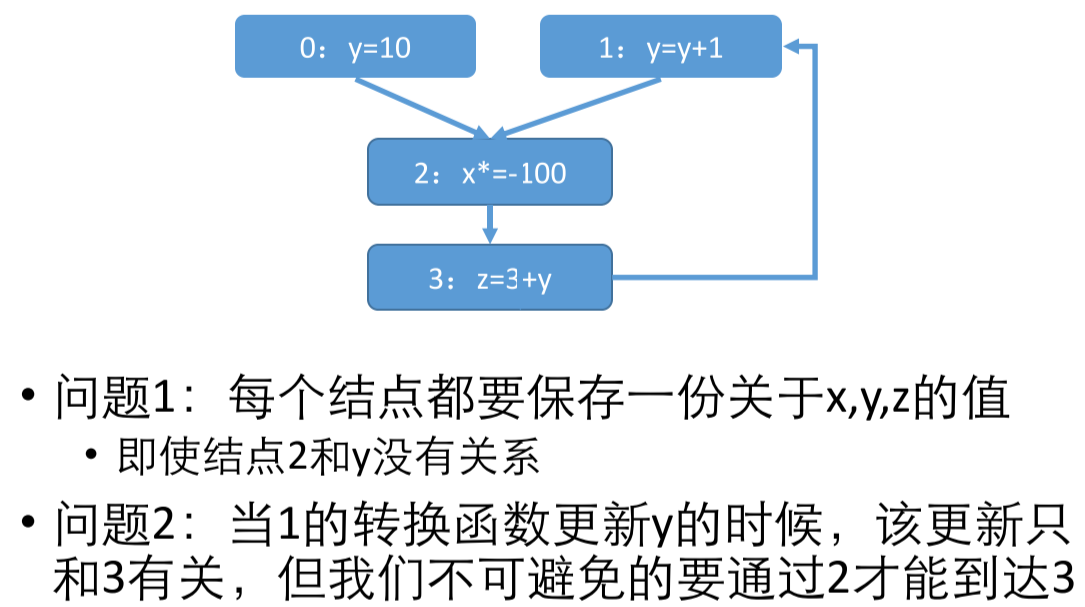
以上的问题其实可以通过思考「Def-Use」关系来解决。
改进数据流分析
其实很容易理解:给定变量 x,如果结点 A 可能改变 x 的值,结点 B 可能使用结点 A 改变后的 x 的值,则结点 A 和结点 B 存在 Def-Use 关系。
如果只是跟踪变量 x,只要跟踪改变了变量 x 和读取了变量 x 的节点即可,中间的不涉及 x 的节点可以忽视。例如,我们分别考虑变量 x, y,那么只要把节点 0-1-3、2 分成两组即可。
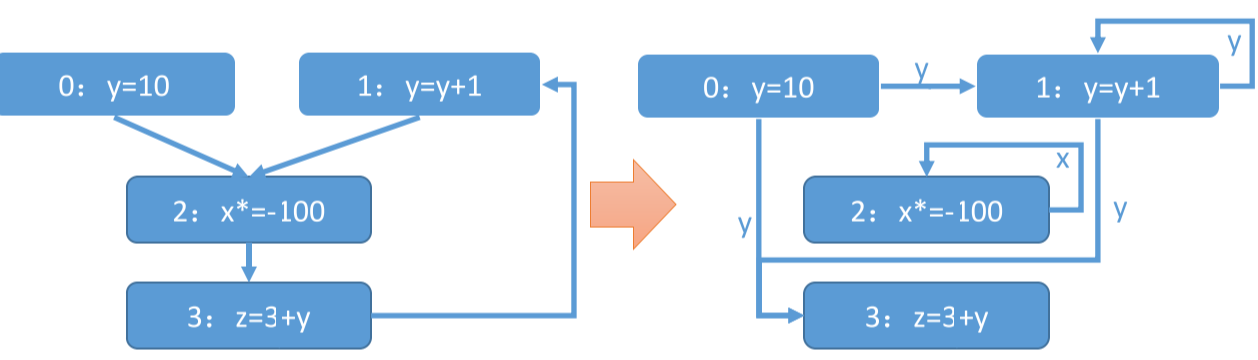
虽然上图看起来更加复杂了,但是对于单独的变量,其实少了中间步骤,生成了更加「稀疏」的图,效率更加高了。总结如下:
- 每个结点只保存自己定义的变量的抽象值。
- 只沿着 Def-Use 边传递抽象值。
- 通常图上的边数大幅减少,图变得稀 疏(sparse)
- 分析速度大大高于原始数据流分析。
- 改进前后的分析结果是等价的。
建立 Def-Use
前面看起来很美好,但是这是基于已经提取了 Def-Use 关系了,但是如何建立呢?实际上这个过程叫做 reachable analysis,而这个过程也是需要静态分析的。具体的例子和程序可以见我写的 《Datalog 和程序分析》 中的应用实例中的数据流分析。复杂度可以参考下图:

另外,**如果定义的变量非常多,改进后的图可能不是更稀疏,反而更加多。**下面是一个例子:
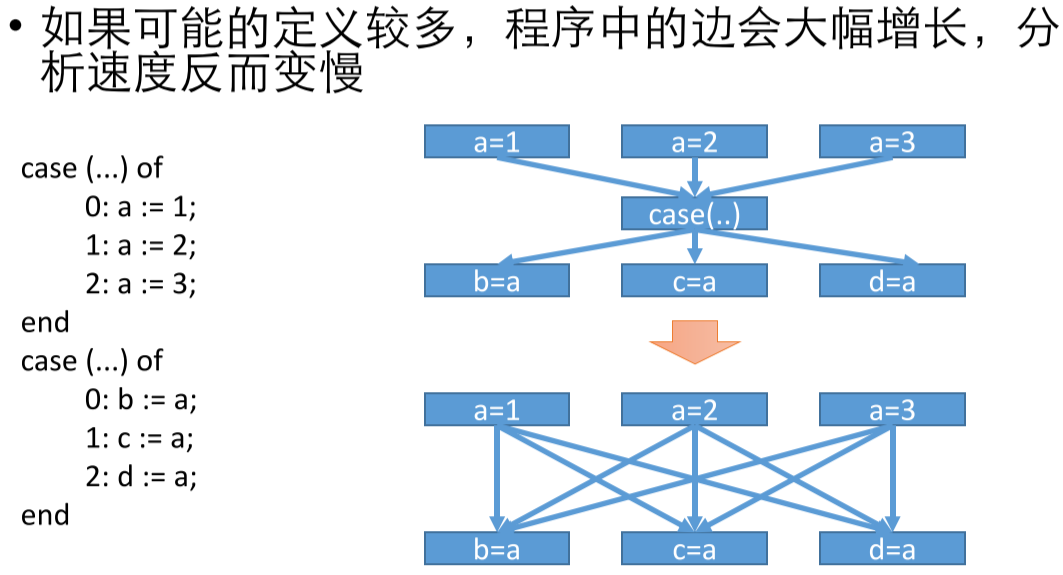
静态单赋值
介绍
核心思想是:每个变量只被赋值一次,多次赋值的时候就当作不一样的变量。其实这里的「赋值」和定义,在程序分析中看起来不怎么区分。比如下面的程序,x+=y 之后的 x 和原来的 x 是不同的变量。

但是不同的分支有不同的赋值行为,比如上述的 z 的值是不确定的。那么引入了 z2=𝜙(z0, z1),表示分支选择,程序分析中表示分支交汇。这样后续就是 x2=x2+z2。
在 Def-Use 之前先进行静态单赋值,得到了右边第二步的结果,这样增加了变量的个数,但是会在第三步起到减少边的个数的作用。
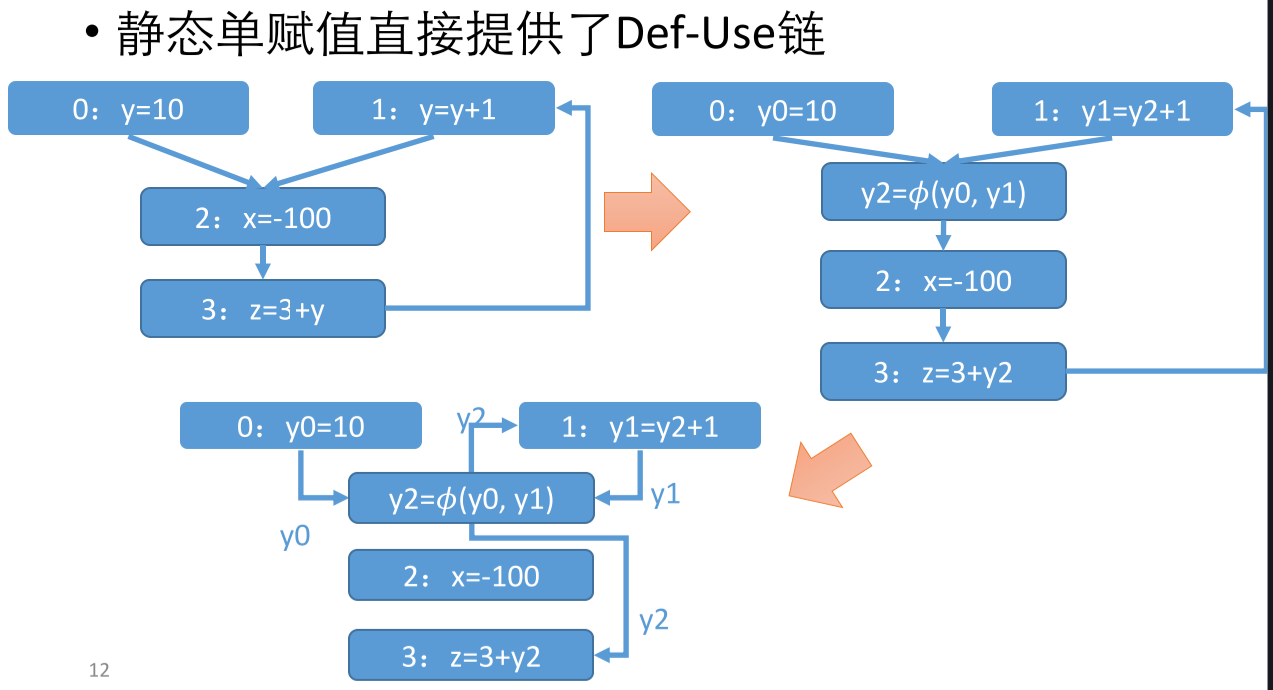
转化成静态单赋值
但是,我们不知道哪些变量该在基本块中汇合。基本块可以理解为一个数据节点,然后汇合是 𝜙 函数。为此,可以在每个基本块中的每个变量都进行汇合。
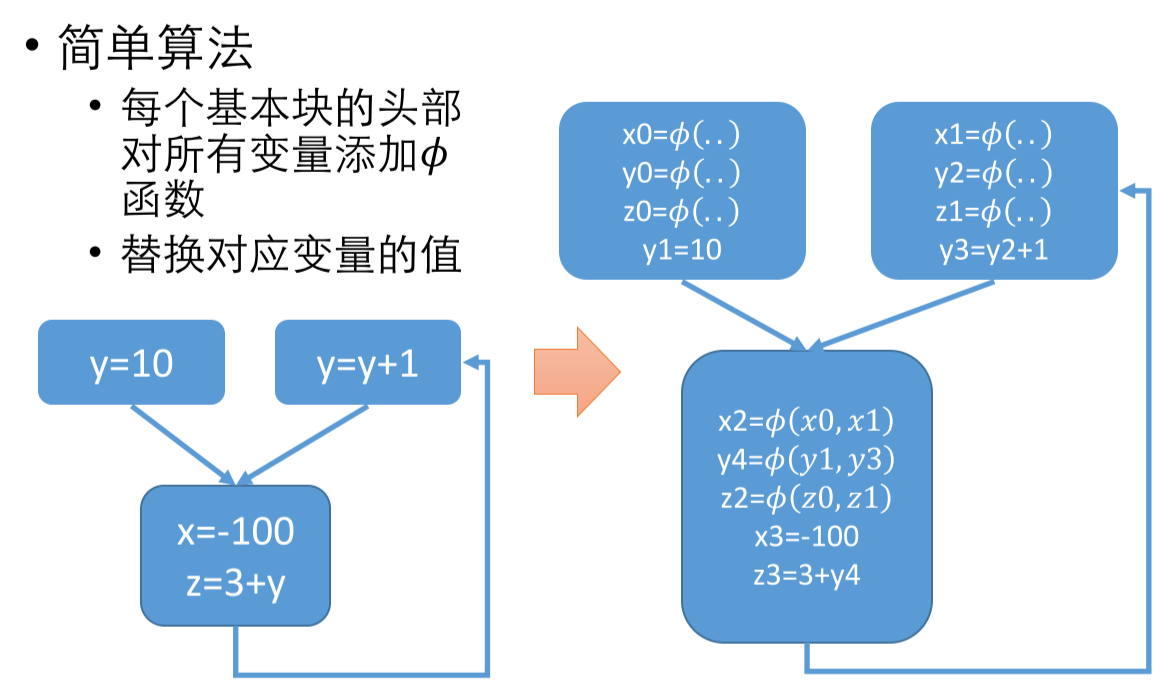
但是显然这很低效,引入了大量没有必要的操作,生成了没必要的新变量。
改进转化
开始探索,**什么时候必须引入交汇函数呢?**已经有成熟的结论了。当且仅当满足如下条件需要引入交汇函数 𝜙:
- 至少两条路径在 B 处汇合。
- 其中一条经过了对 x 的某个赋值语句 S,但存在其他路径没有经过这条赋值语句。
- 语句 S 和 B 之间路径的情况,均不满足条件 1 和 2。
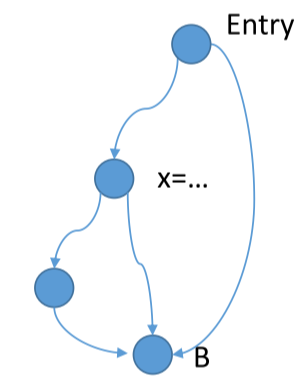
容易理解,即找到最**直接影响 **B 的赋值语句,然后其他分支不会经过这个赋值语句,那么就要交汇。
为了详细说明,引入如下概念:
**支配:**结点 A 支配(dominate)结点 B:所有从 Entry 到 B 的路径都要通过 A。
严格支配:结点 A 严格支配(Strictly dominate)结点 B:A 支配 B 并且 A 和 B 不是一个结点。

容易理解,比如 main 函数中比如会执行的语句抽象为节点,就是支配节点。每个节点都支配自身,比如上图两个都是支配节点,但是只有左边是非支配节点。
不严格支配:至少存在一条路径,在到达 B 之前不经 过 A。
其实可以看出,不严格支配,其实也是不支配了。
支配边界:结点 A 的支配边界中包括 B,当且仅当
- A 支配 B 的某一个前驱结点(注意 A 本身就可以是 B 的前驱节点,任何节点都支配自己)
- A 不严格支配 B
这其实是包含了非循环和循环的两种情况,分别对应上一张图的左边有右边。
定义 DF(A) 为 A 的支配边界集合,其中 A 是节点的集合,也就是说 DF(A) 是集合 A 中每个元素的支配边界的并集,表示如下:
但是如果对一个节点插入了某个变量的交汇函数 𝜙,那么这个节点就相当于增加了新的赋值语句,而这样的行为会影响到后续的节点,因此需要找出闭包。
这样分别对每个节点算闭包,就可以知道每个变量需要在哪些节点交汇了。下面是一个具体例子:
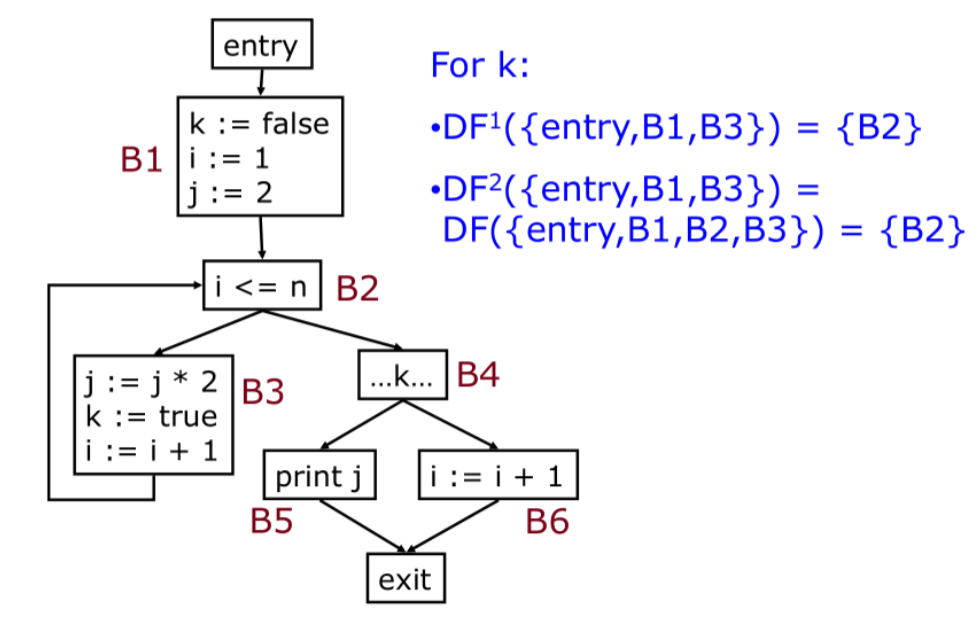
请读者自习回顾「支配边界」的含义,不再赘述。B2 在 B3 的支配边界中。而 B2 支配后续的所有节点,所以支配边界是空集。最后再次迭代,结果不变了,说明已经到达了不动点。
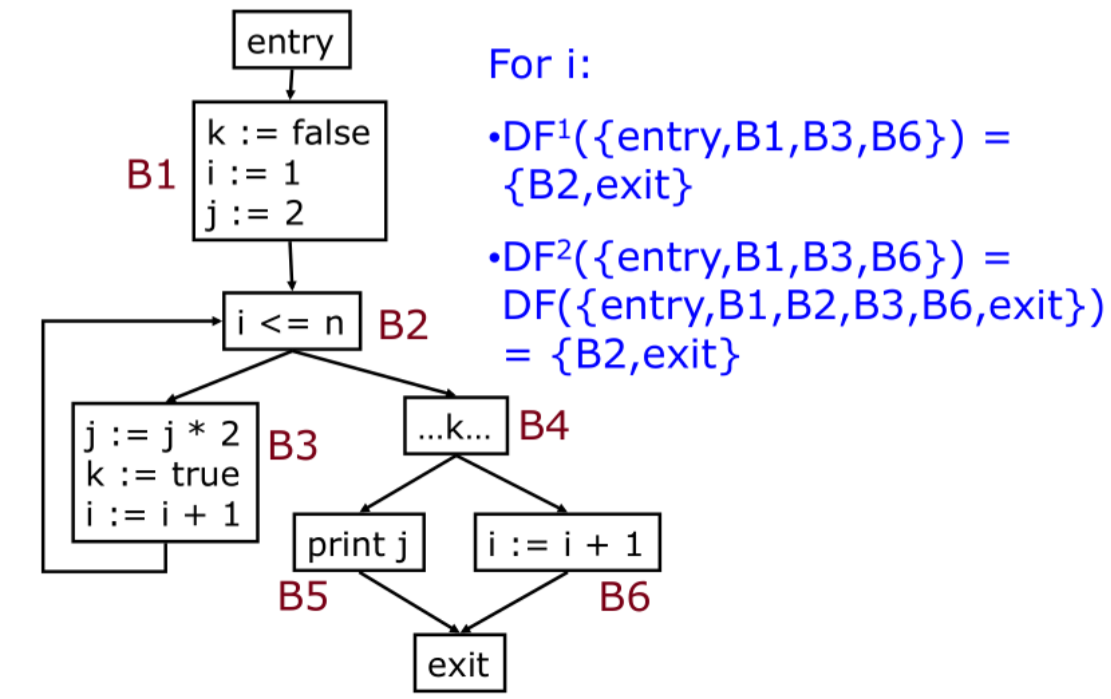
类似地分析即可,B2 在 B3 地支配边界中,exit 在 B6 的支配边界中。
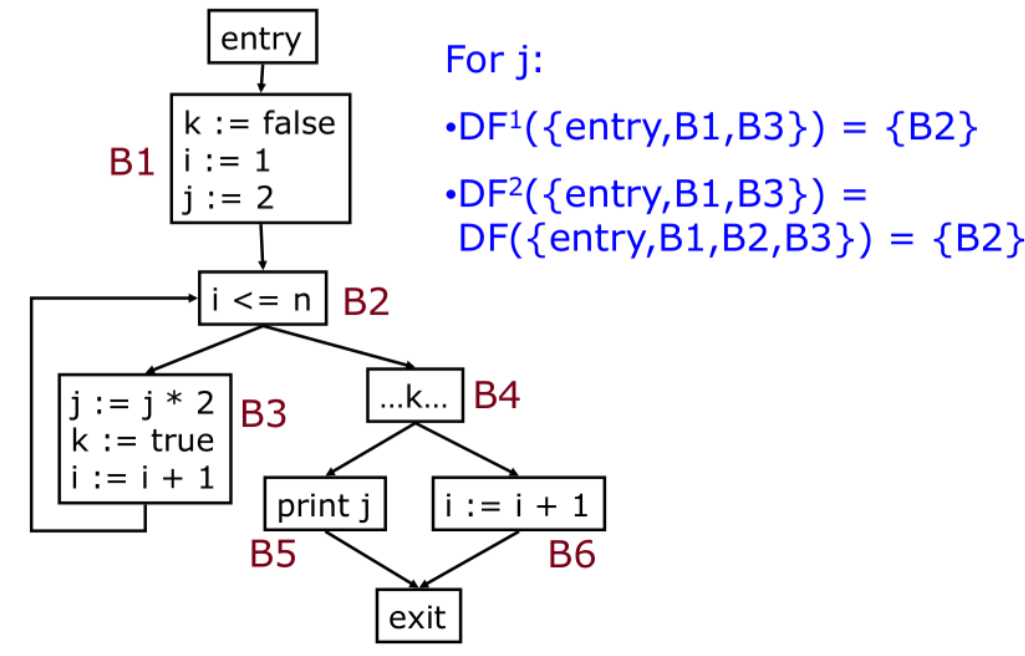
所以最终需要插入交汇函数的结果如下:
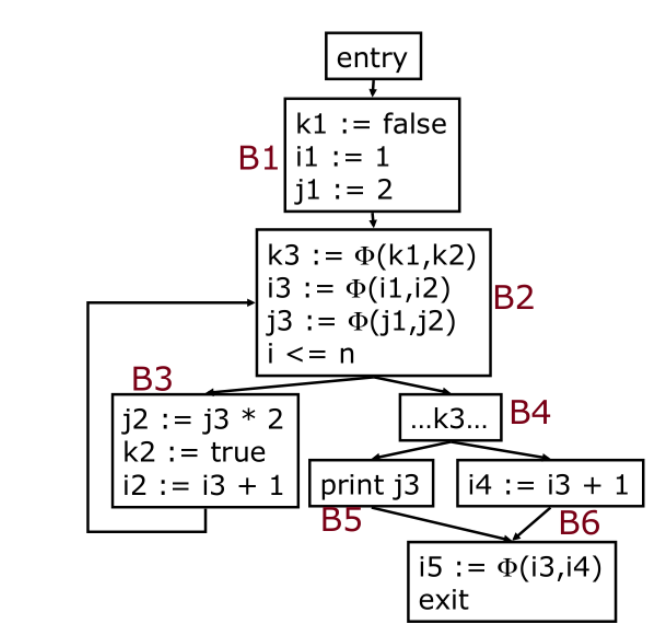
寻找支配边界
首先需要找到直接支配树,定义和例子见下图:
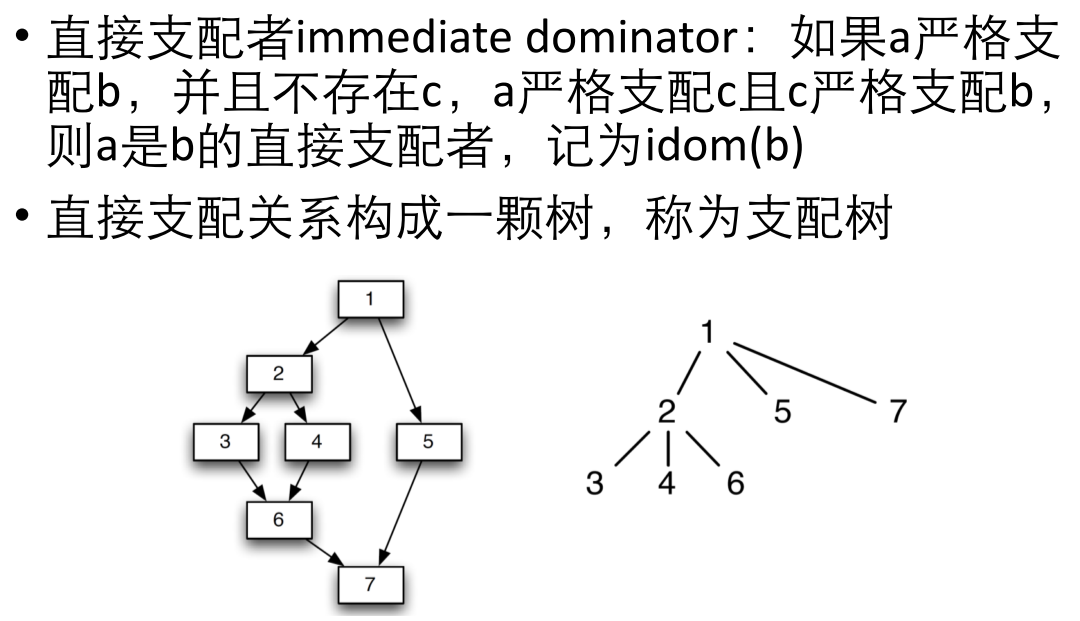
计算直接支配树的主要算法有

然后计算支配边界,流程如下。首先对每个节点 b,至少要有两条路径可以到达它(循环后返回也算作新的路径),这体现为至少两个前驱节点。接着需要找到支配 b 的前驱节点的节点,所以就开始从 b 的直接支配者 runner 开始,然后再去找 runner 的直接支配者,这些支配者的支配边界中都包含节点 b。

一些问题
- 如何转换回标准型
程序优化后,直接删除交汇函数即可。这里我们不探讨逻辑不变性了,比如如果删除某些分支,然后直接删除交汇操作,是否和原来的程序等价呢?
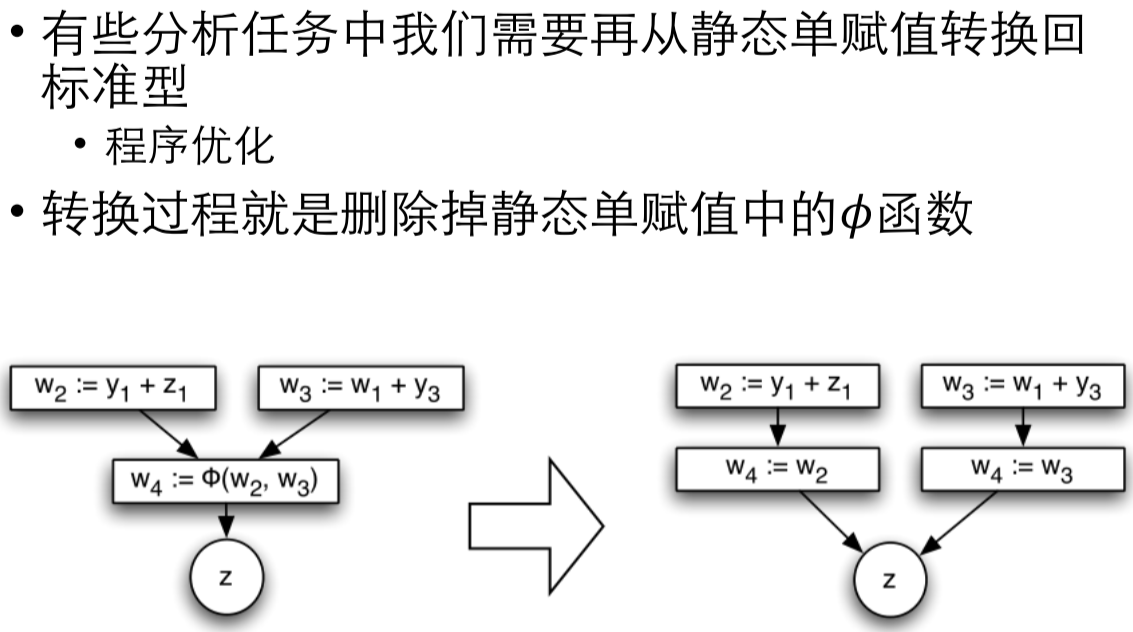
- 实际上,每次赋值的时候,可能变量的内存位置是不变的,只是在原来的内存处读写。而静态单赋值认为不同变量是不同的内存,每个变量对应的内存一旦赋值就不会改变。但是实际情况并不是这样。
为了解决问题 2,提出了 部分 SSA。指针的分析是相对比较复杂的。我们暂时不深入,只要理解我们只对一部分变量进行转化即可。







