（二）数据流分析基础

1. （一）初识软件分析
2. （二）数据流分析基础
3. （三）Datalog和程序分析
4. （四）静态单赋值和稀疏分析
5. （五）过程间分析
6. （六）指向分析
7. （七）抽象解释
8. （八）SMT和符号执行
9. （九）体验静态分析工具
10. （十）Fuzzing 基础

数据流分析

基本思想：程序视作状态和状态的转移两部分组成，忽视状态转移的条件，分析状态转移时的变化。

近似的两种方案：

1. 忽略程序的条件判断，认为程序的所有分支都有可能到达。
2. **控制流分叉合并。**这会大大的减少计算量。

这些性质在后面会解释。

符号分析

思想：对变量进行抽象，分析输入的符号和输出的符号，得到抽象的结果。在此基础上可自定义分类和类似地拓展，用更加抽象和概括的符号。例如，对于整数类型，我们可以分成零、正、负、未知四种输入和结果，而不考虑具体的数值。

按照状态转移，我们可能有多条执行路径能够到达目的点 A。例如，if 语句是典型的区分执行路径的的方式。由于未知结果的函数 func1 和 func2，a 最终的符号可能是正、负或者未知。那么，我们可以得到 2 条可能的执行路径(0、5、1、未知)或者执行路径(0、-1、1、 未知)。这里也体现了忽视条件判断的观点。

int a = 0;
a = func1();
b = func2();
//位置1
if(a > 5){
    a -= 4;
} else {
    a = 1;
}
//位置2
a = b;

我们可以：

1. 进一步抽象，合并数据，将第二步的 5 和 -1 抽象为 “非 0 数”。
2. 在控制流汇合的部分，如 if 执行完后，合并数据，而不是单独视作单独的数据流。

例如，当经过了 if-else 语句之后，a 的值至少是 1，所以可以合并后 a 的值变化是（0，未知，大于 0，未知）

最后，总结一般流程：

1. 确定状态集合：$S=\left\{ (a_1,a_2,a_3,...)| a_i\in D \right\}$, $D$ 是每个子状态或者元素的定义域。
2. 每个执行路径上的每个节点视作状态集合 S 的元素。
3. 确定初始值状态 $DATA_{entry}$，设置执行路径上每个节点的状态默认值 $DATA_{node}=\left( T,T,T,\cdots \right)$，$T$ 表示任何情况，随后的半格理论中会再次说明。
4. 确定节点的状态转换函数 $f_v:\boldsymbol{S}\rightarrow \boldsymbol{S}$，具体的函数规则由每个节点的内容决定。
5. 在控制流汇合处，例如在节点 v 处回合，确定交汇运算 $MEET_v=\Pi _{w\in \mathrm{pred(}v)}\mathrm{DATA}_w$，其中 $v$ 表示当前节点，$pred(v)$ 表示当前节点的前驱节点的集合，所以 $w$ 指的是前驱节点。我们约定，交汇处会覆盖默认值，也即 $a_i\Pi T=a_i$ 。$\Pi$ 表示交汇运算。
6. 如果数据流中某个节点的前驱节点更新了，那么更新该节点。
7. 如果没有任何节点的状态更新，那么结束执行。

如果需要深入探讨这个基本流程的性质，一般会包括以下内容：

• Terminating 终止性。符号分析是否会终止，还是一直循环。
• Confluent 合流。这指的是更新节点时的顺序是否会影响到最终的结果。

以上两者可以笼统的归纳为符号执行方法是否收敛 (Convergence)，这将会涉及数理逻辑中形式系统的知识。

活跃变量分析

Liveness analyze 活跃变量分析在编译器、垃圾回收机制中非常常见。对于给定的程序，对于语句 S，变量 V 定义在语句 S 之前，如果 V 的值在执行 S 语句之后还会被读取，那么 V 就是活跃变量。这里需要额外注意的是，活跃变量并不是根据变量名来区分的，而是根据变量实际代表的对象(例如指针指向的值)来区分变量。

var x,y,z;
x = input;
while (x>1) {
y = x/2;
if (y>3) x = x-y;
z = x-4;
if (z>0) x = x/2;
z = z-1;
}
output x;

例如第四行的变量 y 被覆盖了，那么指向第四行之前的变量 y 和执行第四行之和的变量 y，是不同的变量，而且在 y 的值变化的过程中，原来的 y 没有被读取。所以在第一行确定的变量 y 不是活跃变量。

但是第 9 行的变量 z，是活跃变量，尽管它被覆盖了，但是在覆盖之前读取了 z 的值。

活跃变量的分析属于 may 分析，归纳为活跃变量的变量，在后续的执行中可能就不是活跃变量了，因此，一般从程序结束的出口开始分析活跃变量。

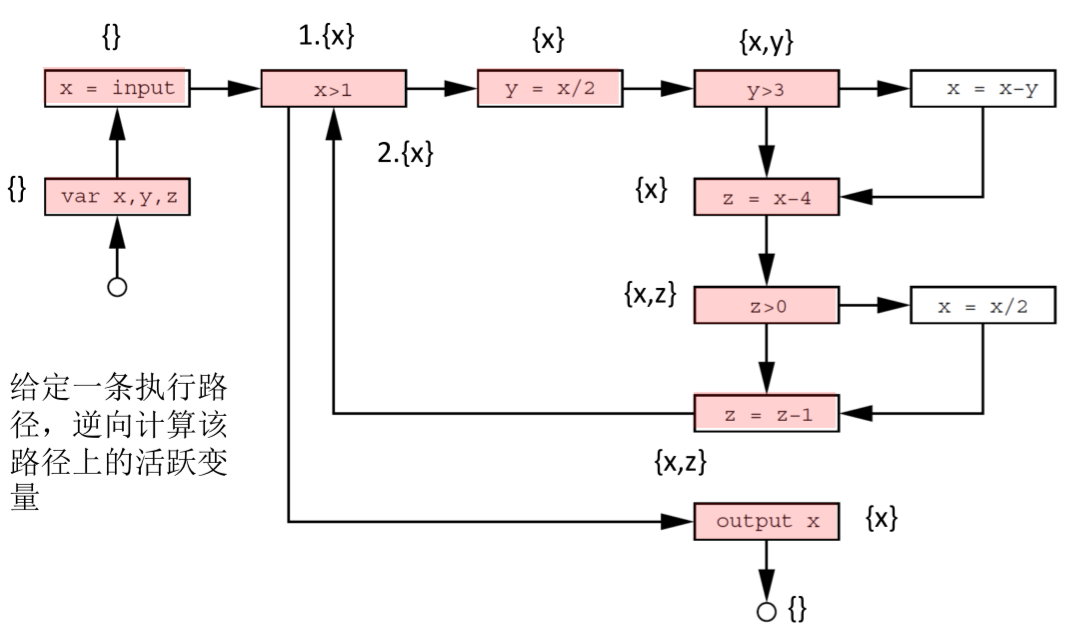
对于执行路径的每个节点，我们给出每个节点活跃变量的集合 ，然后从出口倒着向入口分析，在不同控制流的交汇处取并集，这样就可以得到满足 “变量在当前语句之和会被读取” 的性质。

最后总结一般流程：

1. 初始化出口处的活跃变量为空 $DATA_V=\left\{ \right\}$，

2. 定义从后往前时每个节点的活跃变量的转换函数

   $$f_v(L)=\left( L-\mathrm{KILL}_v \right) \cup GEN_v \\ s.t.\begin{cases} \mathrm{KILL}_v=\left\{ x|x\text{被覆盖} \ \mathrm{or} \ x\text{被重定义} \right\}\\ GEN_v=\left\{ x|x\text{被读取} \right\}\\ \end{cases}$$

   其中 $L$ 表示当前节点从后继节点获取的活跃变量的集合，$\mathrm{KILL}_v$ 是需要在活跃变量集合中删除的变量，$GEN_v$ 是当前节点 v 处产生的新的活跃变量。

3. 交汇处运算 $MEET_{V}=\bigcup_{w \in \operatorname{succ}(v)} D A T A_{w}$，表示后继节点的状态的并集。

4. 更新活跃变量集合 $L_{v}=f_{v}\left(M E E T_{v}\right)$

5. 如果某个结点的后继结点发生了变化，则使用结点更新运算更新该结点的值。

6. 如果没有任何结点的值发生变化，则程序终止。

活跃变量分析需要考虑 sound 和 Convergence，也即严格满足 may 分析，活跃变量集合包含所有可能的活跃变量；活跃变量分析的算法需要收敛。

单调框架

为了确保符号分析和活跃变量分析的收敛性和正确性，提出了数据流分析的单调框架，通过一个通用的可定义的框架，囊括数据流分析基本流程，并且检验每一步的状态转换函数和参数。一般而言，单调框架会涉及到

• 设置节点对应的不同类型集合的统一接口。
• 设置节点转换函数的统一接口。

在开始之前，读者需要明白以下数学内容。

格理论基础简介

格（Lattice）是其非空有限子集都有一个上确界（称为并）和一个下确界（称为**交）的偏序集合（poset）。如果学习过离散数学，那么知道偏序关系是对于 “大于” 或者 “小于” 关系的抽象。

先复习二元关系性质的内容，R(x, y) 表示 x, y 满足关系 R

• 自反性。对于集合 $X$ 上的二元关系 R，若满足：取 $X$ 里任一元素 a，且满足对于所有 a 皆存在 (a,a) 在 R 集合中，则称二元关系 R 是自反的，或称 R 具有自反性，或称 R 为自反关系。例如 a >= a。
• 反自反性。若集合 $X$ 上的二元关系为非对称关系，则

$$a,b\in X,(a,b)\in R\implies (b,a)\not \in R$$

例如 a>b，那么就不会有 b>a。

• 对称性。若集合 $x$ 上的二元关系为非对称关系，则对于所有$ (a,b)\in R\implies (b,a) \in R$。

• 传递性。数学上表示为：

  $$\forall a,b,c\in X,\ aRb\land bRc\;\Rightarrow aRc$$

  例如：大于等于具有传递关系：若 $a\geqslant b$ 且 $b\geqslant c$ 则 $b\geqslant c$

半格 semilattice

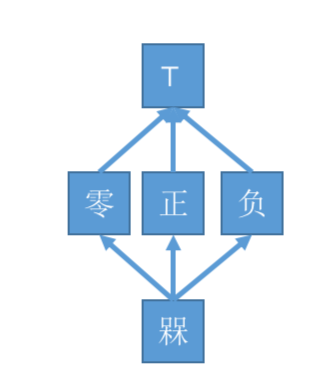
如果理解了「群、环、域」这些近世代数的基本内容，可以很容易的理解这些抽象定义。我们开始理解格和数据流分析的关系。在前面经常提到「抽象」这个词，比如对于具体的符号 +、-，在某个节点中可能同时出现，那么用更加抽象的符号 T 表示。其实，这里的 T 相当于格中的最大元。每一步的抽象类似于偏序关系，构造不同抽象层次的符号集。

**半格的高度：**偏序图的层次数，也等同于半格的偏序图中任意两个结点的最大距离+1。例如下面的偏序图，半格高度为 3

单调框架的基本流程

在有了以上的知识后，我们给出概括性的基本流程：

1. 构建控制流图 (V, E)。请回忆前面我们规定每个语句处视作状态，状态用节点表示，状态之间的联系用节点之间的边表示。
2. 一个有限高度的半格(𝑆,⊓)。「有限」表示控制流会终止，也表示数据流分析收敛。S 表示状态的集合，例如判断数值正负的符号集合，那么 S 包括 {+, -, T}。⊓ 则定义了控制语句交汇处状态汇总的规则。
3. 一个 $entry$ 的初值 $I$。$entry$ 表示初始输入，不同的输入，程序的收敛性和正确性可能不一样。
4. 一组单调的节点转换函数，对除了入口的任意节点 $v\in V-entry$ 存在一个 单调函数 $f_v$。除了初始输入，我们对于每个状态的抽象层次(例如上面提到的 零 正 负和 T。大于表示超集)，使用偏序关系进行排序。采用单调函数以保证偏序关系。

下面是伪代码实现：

1. 程序入口赋初值为 I
2. 除了初始位置的其他节点都赋予默认值 T
3. 初始化未访问的节点集合
4. 如果未访问的节点数量大于 0，那么
   1. 从未访问的节点中选取一个节点 v
   2. 在未访问节点集合中删除节点 v
   3. 交汇节点 v 的每个前驱节点 w, 确定交汇操作。
   4. 如果节点交汇操作输入到节点 v 的状态转移函数后，导致节点 v 的值之前值不同，则更新他的后继节点。
   5. 覆盖节点 v 原来的状态

从上面的流程可以看出来，选取的开始的节点，并不是从初始输入的程序入口处开始执行，这其实是出于考虑状态转换时可能存在特殊的节点，执行到它们后，根据前面提到的规则，可能无法向前驱节点传递状态改变。

小结

数据流分析的性质

最大下界

这一般会在离散数学中学习，在偏序集合中(允许大于等于)，对于某个子集的最大下界，是所有不大于它的元素中的最大元。如下图举例（默认读者理解哈斯图）：如果找 d, e 的最大下界，d,e 的下界有 a,b,c。然后找 a, b, c 中的最大元，由于 a, b, c 没有最大元，所以不存在最大下界。但是如果找 {d, e, b} 最大下界，可以明显的知道是 b。

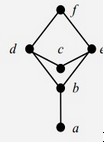
严格定义可以参考下图：

可以看出，半格是特殊的偏序关系，所有元素都存在“大小关系”。

数据流分析的安全性

安全性体现为保持 sound，也就是不会出现 false positive 但是可能出现 false negative。交汇的操作后的值会比单独的每一条路径在此节点的值更小。这里嵌套的状态转移函数表示从入口到节点 $V_i$ 的状态转移过程。严格的定义如下：

如果考虑到路径上的节点其实也可能进行了交汇操作，上面的结论是否还是成立呢？其实只要满足前面小节中变化函数是单调函数，而且交汇函数形成半格即可。详细说明如下：

数据流分析的分配性

分配性是为了克服 false negative 提出的。分配性的定义：一个数据流分析满足分配性，如果

$$\forall v \in V, x, y \in S: f_{v}(x) \sqcap f_{v}(y)=f_{v}(x \sqcap y)$$

可以发现，安全性可以理解为右边小于等于左边。可以通过集合运算验证是否满足分配性，注意观察下面的结果是等号而不是被包含，另外要理解即使满足了分配性，数据流分析可能还是近似的，因为节点的状态转换函数还是可能是近似的。我们略过证明过程。

数据流分析的收敛性

由于数据流分析的基本原理是交汇操作和节点转换函数，再结合基本条件中节点转换函数必须是单调的，因此随着路径地加深，而半格高度有限，必然会逐渐收敛。可以证明，收敛到不动点，且它一定是最大的不动点。

widening and narrowing

它的提出是为了解决数据流分析的复杂性，太过复杂会导致收敛速度极慢。

区间分析

以区间分析为例：

可以想到的是，如果正向进行，变量的范围应当是逐渐扩大的，即交汇操作满足 $$[a, b] \sqcap[c, d]=[\min (a, c), \max (b, d)]$$变换函数表示这条语句自身导致变量的变化，例如加上一个变量或者变量组合。

$$\begin{aligned} &{[a, b]+[c, d]=[a+c, b+d]} \\ &{[a, b]-[c, d]=[a-d, b-c]} \end{aligned}$$

但是这样构成的半格高度是无限的，而且操作也不能保证单调性，因此提出了改进策略——人为指定上下界。如果下界大于类型的最大值，那么为空值，程序异常；如果下界小于最大值，那么更新下界和上界，其中如果最大值之和和类型最大值取其中小者。

$$\left\{ \begin{matrix} [a,b]+[c,d]=\varnothing& a+c>\mathrm{int}_-\max\\ \left( a+c,\min \left( b+d, \mathrm{int}\_\max \right) \right)& a+c\le \,\,\mathrm{int}\_\max \\ \end{matrix} \right.$$

基础 widening

但是这样做的复杂度还是很高，于是可以通过降低结果的精度来加快收敛速度。基本的 widening 的方法是降低格的高度，它的核心是把结果进一步抽象，通过单调函数 $w$ 把原来的半格映射成新的格，也即$f\gets w\circ f$。例如在区间分析中可以预定范围，

• 定义有限集合：$$B=\left{ -\infty ,10,20,50,100,+\infty \right}$$
• 定义映射函数 $w$：$w([l, h])=[\max \{i \in B \mid i \leq l\}, \min \{i \in B \mid h \leq i\}]$

这样就可以把区间 [15, 75]、[11, 89]等等映射成 [10,100]，也即 $𝑤([15, 75])= [10,100]$。由于状态数大幅减少，所以很大程度上加快了收敛速度。

再比如，对于如下代码我们比较是否应用基础 widening 的区别：

y=0;
while(input){
    x = 7;
    x = x+1;
    y = y+1;
}

补充：需要理解什么是交汇的节点，比如循环的入口就是，可以理解为执行路径的交点。

有限集合为: $$\left{ \mathrm{−}\infty ,0,1,7,+\infty \right} $$，每次循环第二行处的状态如下图所示：

基础 widening 的安全性和收敛性

安全性需要保证：$w(x) \sqsubseteq x$ 这是容易确定的，因为原来的 $f(x)$ 是单调的，那么构造合适的 $w$ 即可。

收敛性由单调性容易得到保证。

一般的 widening

基础的 widening 的精度不高，而且精度和收敛速度是不能两全的，但是一般的 widening 方法可以在一定程度上提高性能。一般的 widening 同时参考更新前和更新后的值来猜测最终会收敛的值。设 widening 算子 $\nabla $，它是我们自定义的规则。那么推断节点新的值可以表示为：

$$\text { DATA }_{\mathrm{v}} \leftarrow \text { DATA }_{\mathrm{v}} \nabla \mathrm{f}_{\mathrm{v}}\left(\mathrm{MEET}_{\mathrm{v}}\right)$$

再次以之前的代码为例，但是我们更改规则

y=0;
while(input){
    x = 7;
    x = x+1;
    y = y+1;
}

节点交汇操作规则如下，其中 T 表示格的最高层的元素

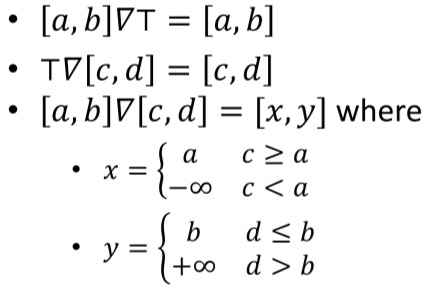
可以对比分析以上提到的不同的方式：

一般 widening 的安全性和收敛性

为了保证安全性，构造 widening 算子的时候需要注意：

$$(x\nabla y\sqsubseteq x)\land (x\nabla y\sqsubseteq y)$$

但是为了保证收敛性比较麻烦，没有通用的判断方法，因为 widening 算子与变换函数的趋势有关，也无法保证在半格上的单调性。

这里提及一种不收敛的情况，当多条路径交汇的时候，如果定义的交汇操作时逐个进行的，那么可能由于处理前驱节点的顺序不一样，造成不一样的结果。

narrowing

widening 是只产生的区间比实际的区间更加大，而 narrowing 会将区间变小。通过再次应用原始转换函数对 Widening 的结果进行修正，narrowing 的方法可以提高 widening 的精度。简单的说，就是在某一步就不采用 widening 的方法，而是用原始的函数。例如下图 x 的值的区间在第 5 步突然缩小了。

引入 narrowing 算子 $\Delta$：

$$\mathrm{DATA} _{\mathrm{v}}\gets \mathrm{DATA}_{\mathrm{v}}\Delta \mathrm{f}_{\mathrm{v}}\left( \mathrm{MEET}_{\mathrm{v}} \right)$$

例如算子定义如下，当区间出现无穷时，可以缩小区间。

narrowing 的安全性和收敛性

这里核心是需要证明在 widening 基础上再使用 narrowing，也是安全的，保证不会出错。根据前面的定义，初始输入 $I$ 经过任意路径上的多个状态转换函数后得到的值的交集（按照半格顺序取小），会大于交汇操作得到的值。而经过 widening 映射后的新的半格也会满足单调性，并且每个节点的值必须小于初始的的值。按照下图，可以知道即使是从 widening 后的不动点 $I_G$ 再使用原来的转换函数若干次，得到的值会比 widening 的更小(精确)。

简单地说，如果算子满足如下条件就是安全的：

$$x\Delta y\sqsubseteq y$$

narrowing 是不保证收敛的，即使收敛也不能保证能够快速收敛。

根据上图可以知道，使用 narrowing 后的结果是在两个不动点之间，但是无法判断是否收敛。