(五)过程间分析
之前我们所有的分析都是没有函数调用的,也就是之前考虑的情况都是「过程内」的调用。本章将会考虑函数调用,开始「过程间」分析(Whole Program Analysis 或者 Link-time Analysis)的学习。
基本思路
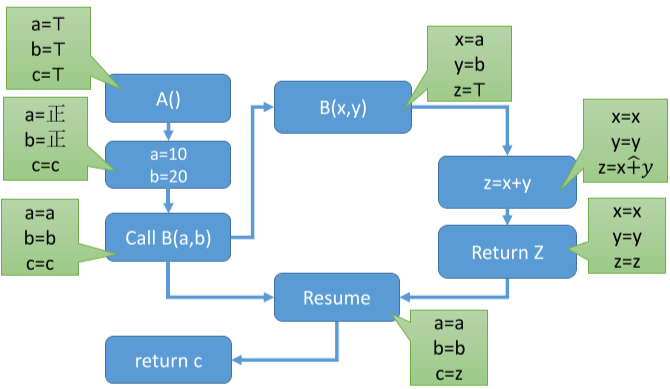
每个过程内分析对应一个抽象域,然后函数调用时,每个函数都是新的过程内分析。那么,只要考虑两个过程内分析的衔接即可。例如对下面的程序,在函数 A 内调用函数 B 时,其实就是过程间分析,调用和返回时对节点进行转换即可。
1 | int B(x,y){ |
全局变量
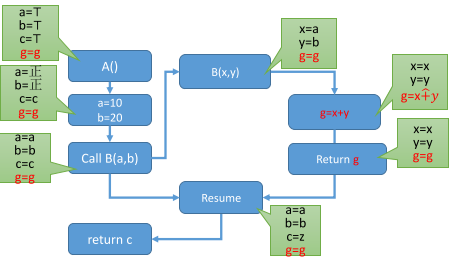
如果出现了全局变量就会比较麻烦,那么过程间分析如何处理全局变量呢,一个办法是在所有的基本块中都添加全局变量,或者可以改进,只在读写了全局变量的过程内调用和调用了这个函数的地方添加全局变量。这其中比较烦的问题是,如果函数调用的层级比较深,那么其中的每个函数都要增加全局变量。例子如下:
1 | int B(x,y){ |
精度损失
假设 A 和 C 都调用了函数 B,然后也是采用 调用-返回 来执行过程间分析,那么函数 B 中变量改变了,又同时作为 A 和 C 的前驱节点,这样假如 A 改变了,那么 B 作为后续的过程也会发生改变,同时函数 B 中有 C 的前驱节点,C 也要重新评估。也就是说,只是因为调用函数 A,却导致了函数 C 的值也发生了变化。
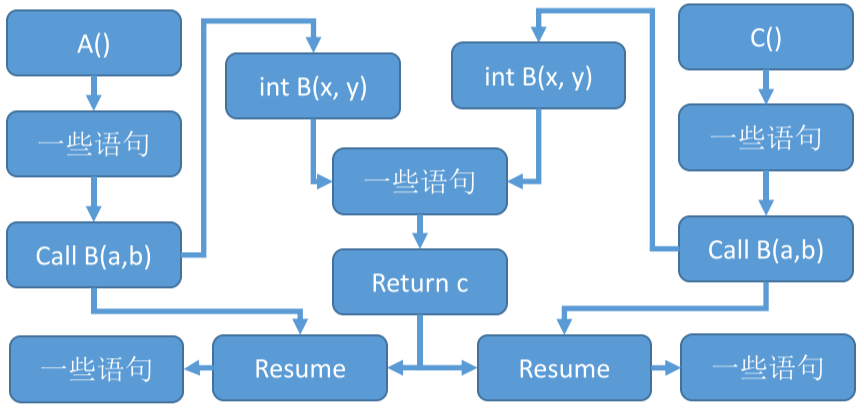
由于这种失真的触发条件非常容易,只要一个函数同时调用两次,就会出现问题,导致程序分析的结果非常不准确。
克隆和上下文敏感性
上下文指的是语句所在的环境,比如前后的语句和变量。上下文非敏感分析(Context-insensitive analysis) 在过程调用的时候忽略调用的上下文,因为上下文不会影响结果。上下文敏感分析 Context-sensitive analysis 则需要考虑上下文。类似的,控制流敏感只是把上下文改成了控制流中的分支,定义类似。
更加直接地理解,上下文不同的函数可以理解为不同调用位置的函数。特别地,对于递归函数,输入不同,那么上下文可能不同,有无限可能。所以,尽管递归函数在一个位置调用,但是从控制流的角度,上下文随着输入的不同,是不一样的。
为了解决上面的问题,很直观的想法是,在上下文敏感的调用位置处,都克隆一遍这个函数,让各处调用没有联系。
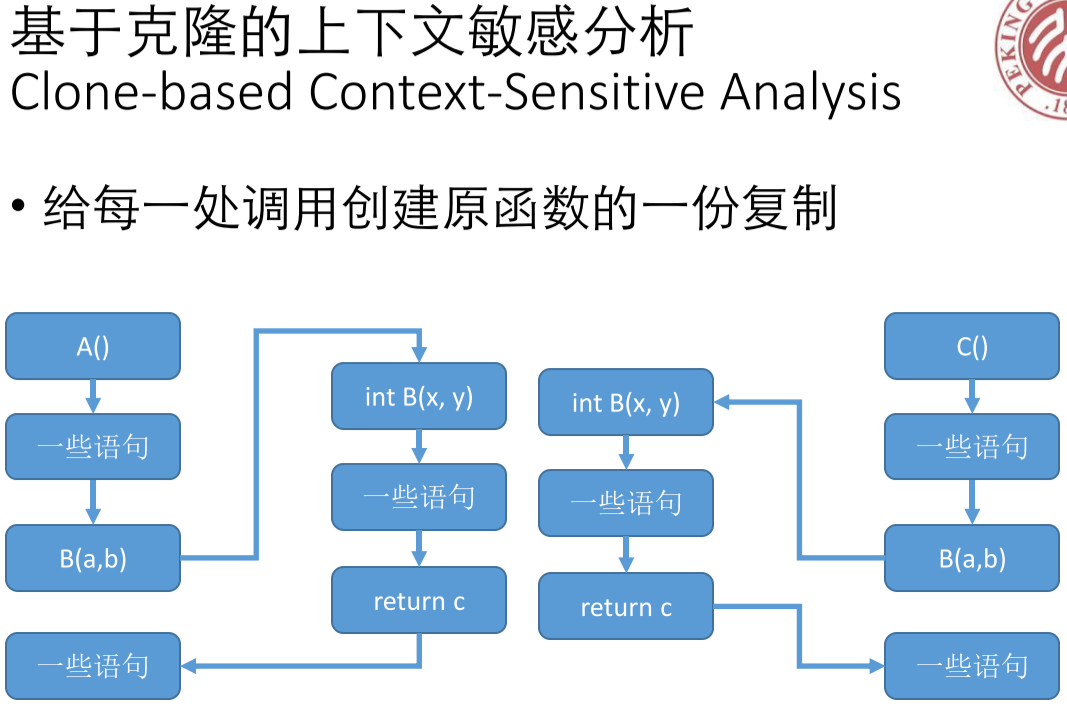
克隆的问题
但是,对于嵌套的函数,比如 A 调用 2 次 B,B 调用 2 次 C,C 调用 2 次 D。如果只是调用 A 一次,那么需要克隆 2*2*2=8 次 函数 D。对于一些面向对象的语言或者函数式语言,克隆发将会带来很大开销,根据调用深度指数增长。
另外,对于递归函数,自身无法静态地确定调用的次数,而且克隆次数非常多。无法处理这种情况。
为了解决上面的问题,提出了两种方案。

如果读者没有理解「上下文」的含义,请回顾上一小节。解决方案 1 容易理解,解决方案 2 通过下面的例子学习。首先看明白递归函数的控制流图:
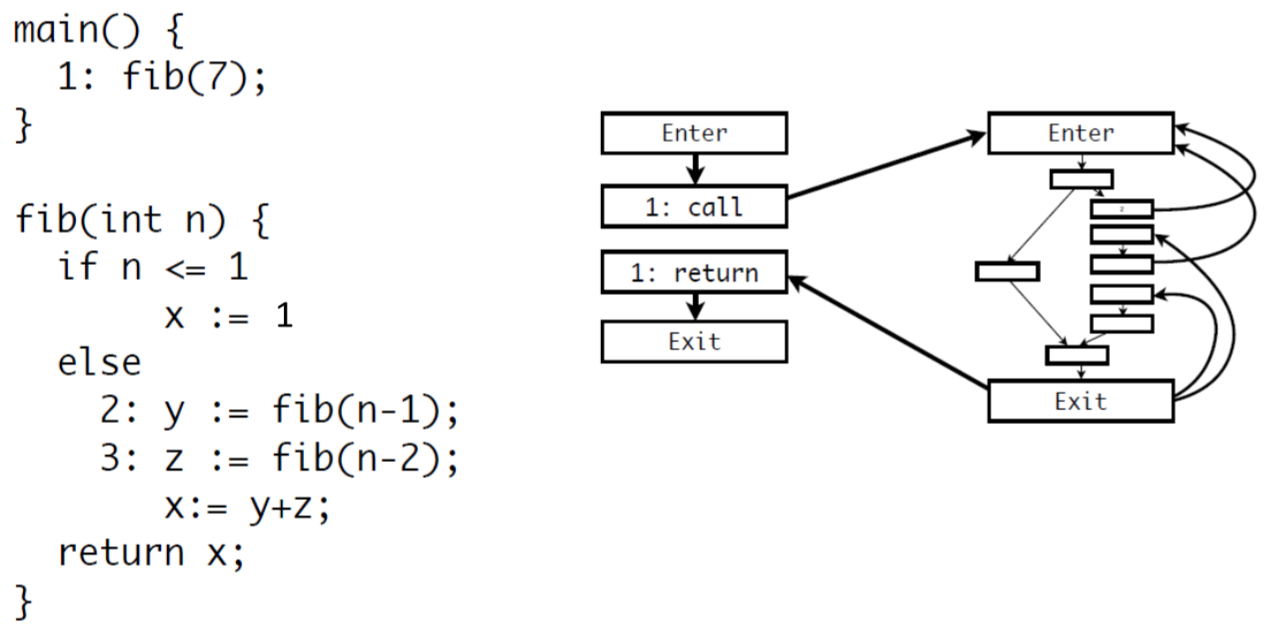
笔者也不想重新画这个图,于是结合文字理解吧。Enter 入口之后是一个分叉,表示控制分支。分支坐标是赋值语句,然后是 return 处的交汇,接着就退出函数。
右边首先是 2 号位置的 fib 函数,会递归调用自身。然后直到走左边的分支,从 Exit 最右边的线,返回到右边一列的第二个方格,然后给 y 赋值,接着进入 3 号 fib 函数,同样直到走左边的分支,然后从 Exit 进入右边倒数第二个的方格,接着给 z 赋值,再计算 x=y+z,最后交汇运算,Exit,完成整个调用。
然后,我们再看下面调用深度为 1 的情况。标号在代码中,context 1 是 main 函数中的调用,结束后直接返回即可。context 2 表示 2 号调用,有三个入口,一个是初始的调用,一个是自身的反复调用,一个是来自 3 号的调用。context 2 的调用结束之后,开始 3 号的调用。context 3 则有 2 个入口,分别是调用完 2 号后到 3 号,还有是直接在 context 1 中的调用。
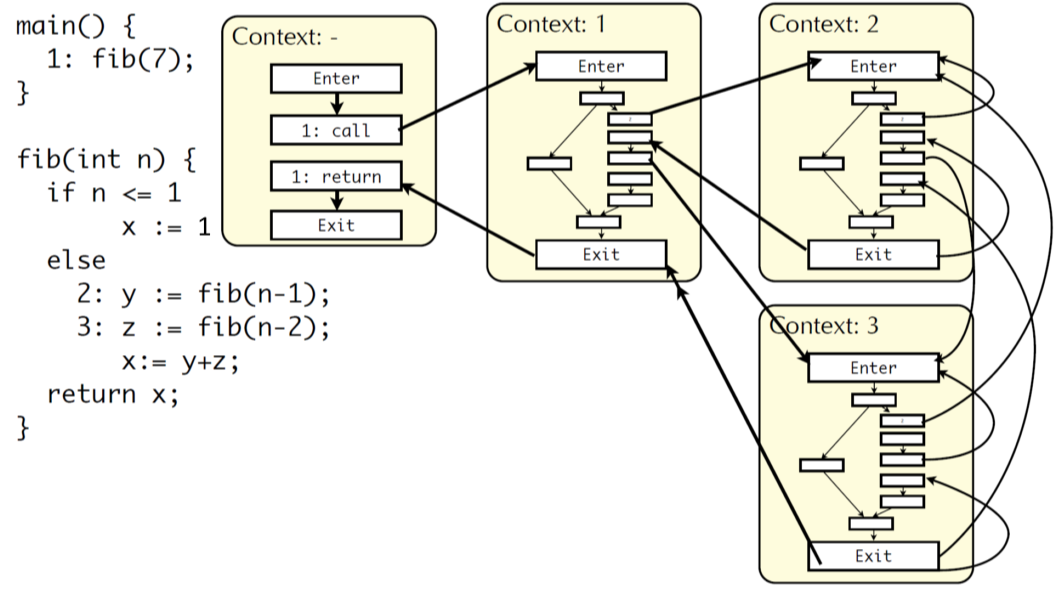
递归调用肉眼可见的复杂,主要是要理解三个上下文对应的情况,读者不理解的话,可以多次琢磨。下面是两层的情况,读者直观看一眼,理解方法即可。
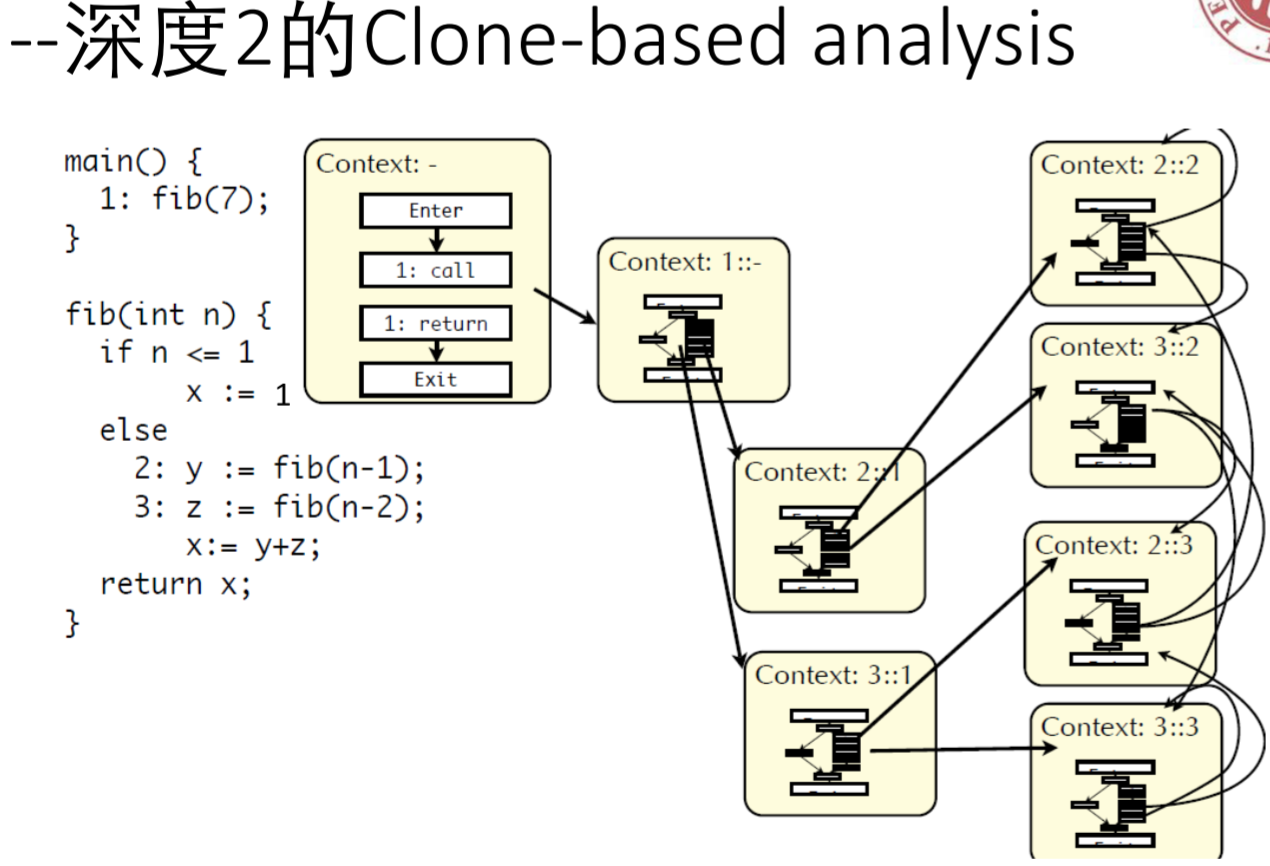
总的来说,递归函数调用深度越深,那么分析越准确,但是复杂度指数上升。
不同的上下文类型
以上的讨论都是基于调用位置的上下文,但是在具体分析的过程中,会设置不同的上下文定义,方便各种不同的分析。
- 基于函数名字而不是调用位置的上下文。不如调用位置精确,但能减少复制量。
- 基于对象类型的类型的上下文。在面向对象语言中,对于
x.p()的调用,根据 x 的不同类型区分上下文。比如接口类型或者函数重载,就会出现 duck type. - 基于系统状态的上下文。根据分析需要,对系统的当前状态进行分类,当函数以不同状态调用时,对函数复制。
克隆的例子
数据流分析默认所有分支可达,但是如果实际上可能会出现互斥的情况。例如下面的代码,因为 condition1 和 condition2 互斥,所以只有如下几种调用情况 x n 或者 y m,按照之前的做法,每个分支都会交汇,造成了允许 x m 这种不可能的情况。
1 | condition1 = not condition2 |
但是,如果通过克隆的方法,不局限在克隆函数,自定义上下文为「第一个 if 语句的条件为 true 还是 false」,那么克隆第二个 if 语句,上面的式子可以写作:
1 | condition1 = not condition2 |
克隆之前之前,会分别跑完 x(),y(),然后在 x(), y() 的出口处,对全局变量进行交汇操作(用静态单赋值算法确定需要交汇哪些变量),之后再执行第二个 if 控制流;
克隆之后,只会分别执行x() , y(),例如执行完 x() 之后,再执行 m(),n(),在出口处交汇第二个 if 执行的全局变量。最后再分别交汇第一个 if 的两个分支。
课件里说第二种情况会更加精确,笔者理解为,第二种情况在执行 m()、n()的时候,上下文会更加精确,具体来说是全局变量的值更加精确。但是多了一次第一个 if 结束的交汇操作,笔者就有点扯不清了。后续深入学习或许会从理论角度来填坑。
除了上面提到的是基于系统状态分类的语句级别的复制。之前举的递归函数的例子,或者循环的例子(类似递归,可以展开 k 层,上下文是上一层循环和下一层循环)都是 clone 方法的应用。
实际上,克隆的方法等效于 inline(内联:把被调函数的代码嵌入到调用函数中,对 参数进行改名替换)。
精确的上下文敏感分析
以上提到的分析,都是因为过程间调用(比如函数调用)会导致其他调用的地方意外地更新节点,提出了基于克隆的的方案。考虑到递归、多次循环等上下文非常复杂,只是局限在前 k 层分析。但是,精确的上下文敏感分析的目标就是,让每一次调用都和上下文匹配,也就是说,对于任意分析中考虑的路径,路径中的调用边和返回边全部匹配(称为可行路径)。
历史上提出过多种精确上下文敏感分析方法
- Functional
- Dataflow Facts-based Summary
- CFL-reachability
近年来的研究逐渐集中在 Thomas Reps 提出的 CFLReachability 上,优点是:
- 理解上比较直观,可以画图说明。
- 能够优化出高效算法
- 能覆盖任意的具备分配性的数据流分析(但不能覆盖所有已有方法)
- 基于该模型讨论清楚了若干可判定性问题。
在解决具体问题之前,先了解 Dyck-CFL,其中 CFL 指的是 Context-free language,我暂时不是很熟悉编译原理,所以不深究。维基百科介绍如下:
In formal language theory, a context-free language (CFL) is a language generated by a context-free grammar (CFG).
Context-free languages have many applications in programming languages, in particular, most arithmetic expressions are generated by context-free grammars.
而 Dyck 语言是基于括号匹配的语言,具体见 wiki。最关键的介绍是,用于判断嵌套的括号是否匹配。
In the theory of formal languages of computer science, mathematics, and linguistics, a Dyck word is a balanced string of square brackets [ and ]. The set of Dyck words forms the Dyck language.
Dyck words and language are named after the mathematician Walther von Dyck. They have applications in the parsing of expressions that must have a correctly nested sequence of brackets, such as arithmetic or algebraic expressions.
那么,在每一处过程间调用的入口,都根据上下文调用和返回,做括号的匹配,就会涉及到 Dyck CFL ,确定嵌套的括号匹配必须正确,让程序分析只跑括号正确匹配的路径(可行路径)。
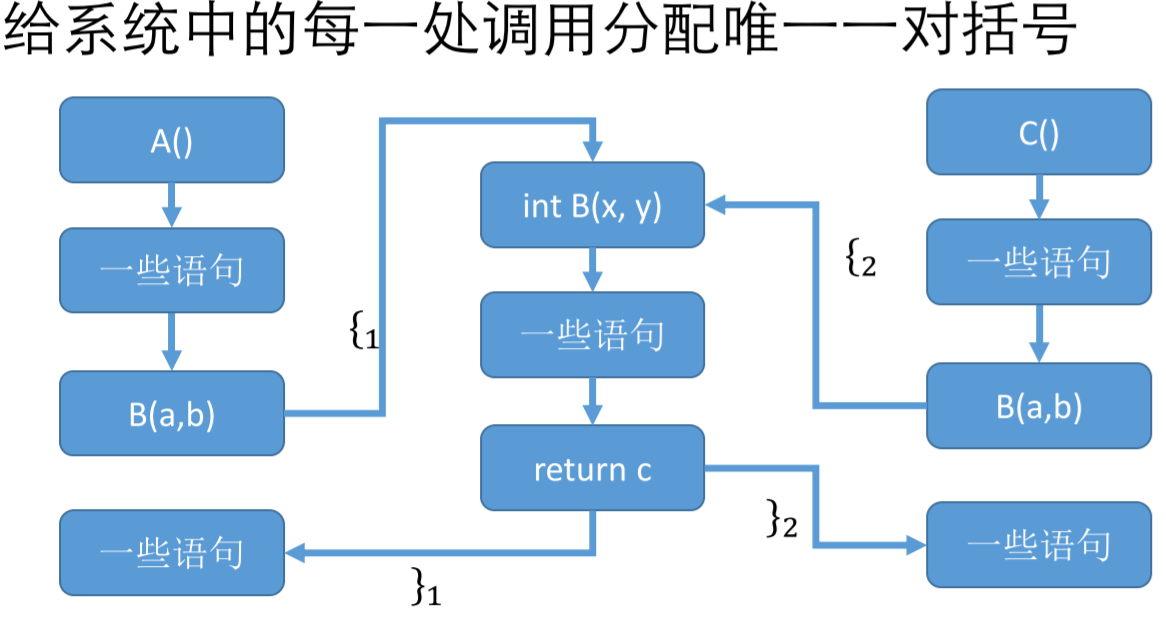
回顾数据流分析的分配性:
结合数据流分析的过程,可以容易得到如下的推论:

这就导出了一个非常有意思的结论了,如果数据流分析满足分配性,我们可以把初始值 A 拆成多个不同的初始值 B C D 的交汇,那么不好处理的初始值 A,就可以转换成好处理的初始值 B C D,任意一个数据节点的值也可以由 B C D 对应的数据节点交汇得出。
一般地说,KILL-GEN 这种标准的数据流分析是满足分配性的。下图来自 https://karkare.github.io/cs738/lecturenotes/03DataFlowAnalysisHandout.pdf

我们抽象出来函数
那么全集 U 的子集为
的结果必然在子集之中,并且存在输入到输出的对应关系
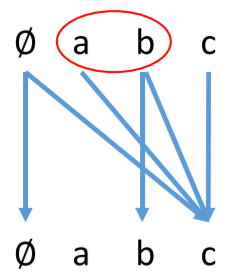
当 x 取集合 {a, b} 时,根据分配性,只需要交汇 f(a) 和 f(b) 即可,假如交汇是取集合并集的话,那么就把 a 对应的集合和 b 对应的集合取并。虽然以上只是进行了一步的状态转换,但是多次转换也是同样的原理。这样就将数据流分析转换成了一张图。
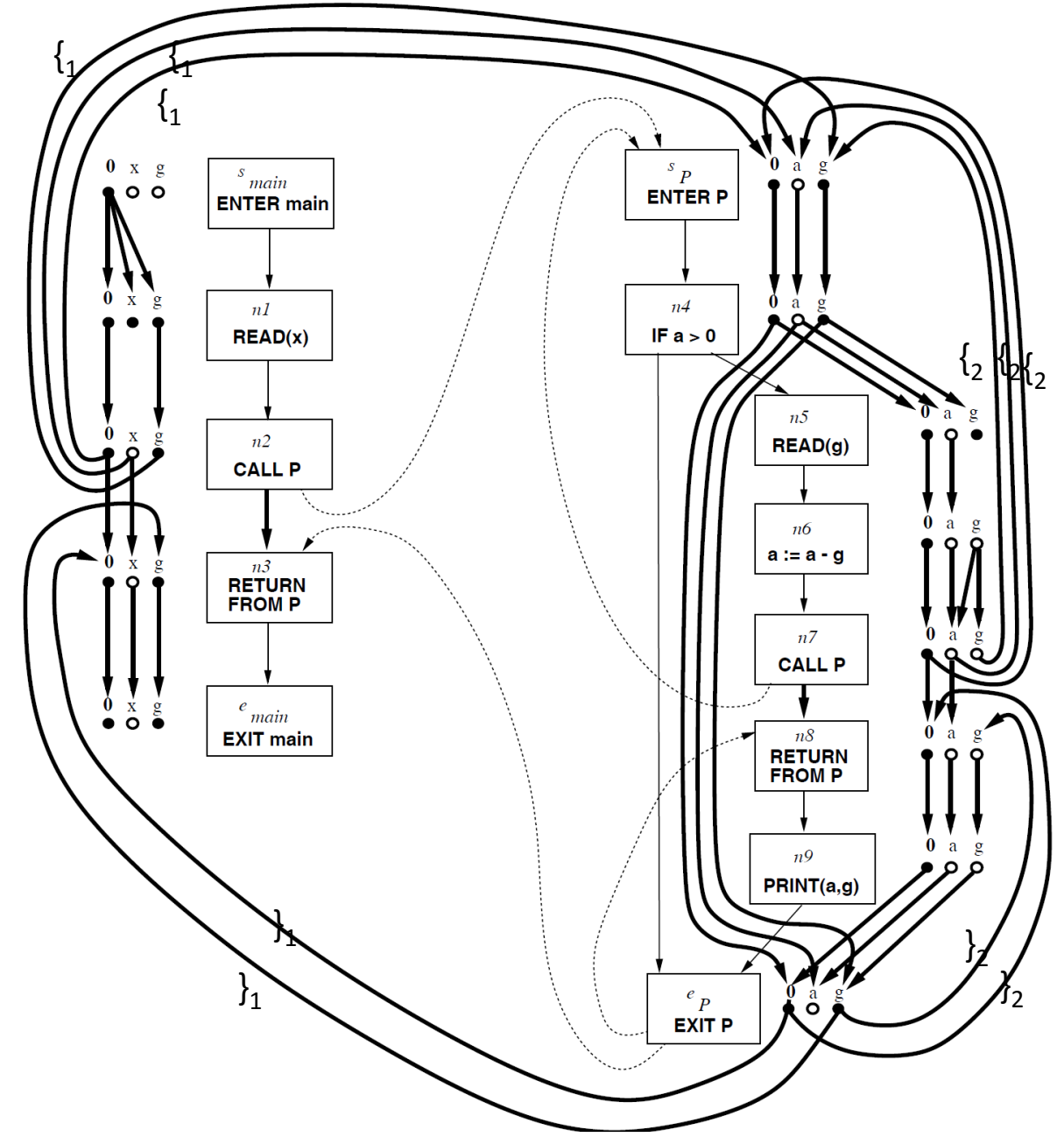
下面是分析未初始化变量的图,READ 表示从键盘读取然后写入变量。节点转换的连线表示输入的节点,就会影响输出的节点是否初始化,这样的映射关系也就是状态转化函数。
首先,x, g 从读取空值,也就是没有初始化。然后 x 被赋值,所以不再影响下一个个节点。接着进入调用 P,先标记左括号 1。注意,每个节点并不知道自己的数据是否是未初始化,只知道节点转化的规则。进入调用 P 后,标记左括号 2。在节点 n5,从键盘读取了数据写入 g,所以从变量 g 开始的边断了。节点 n6 处 a 或者 g 未初始化,那么 a 就会未初始化。
未初始化的变量,就是从入口开始,通过有向图可以到达(条件包括路径可达和括号匹配)的任意节点处的变量,就有可能是未初始化的变量。这就将数据流分析转化成了图可达性问题。
注意到 n4 分支处交汇,如果直接交汇,忽视了分支,其实还是会比较可惜,日后会学习更加精细的做法。
下面是上下文无关语言钟正式一些的可达性定义:

而可达性在 Datalog 中很容易推导。最直接的算法就是加边,递归的按照下面的三种方式加边,如果有直接相连的边,那么就是可达,虚线表示可达。

加快分析速度
过程间分析相较过程内分析,是非常吃性能的事情,动则分布在几十个文件中几万行的代码互相调用,所以编译器一般都会默认关闭过程间分析。加快分析速度也是较为重要的问题。比如克隆的部分如果特别大,那么程序分析的开销就是非常大。
加速技术主要有两类,动态规划也就是记忆化搜索,比如 A->B->C->D,可以在搜索时记忆 A->C 是成立的,然后只要判断 C->D 是否成立即可。实际上也还有其他的形式。
另外一种就是函数摘要,函数调用往往存在嵌套的调用,A() 在内部调用 B(),B() 在内部调用 C() D(),如果每一次都遍历到最底层的函数,那么将会耗费大量的时间。因此可以合并函数内部的函数,特别是库函数重用很多。而且如果源代码改变,摘要不需要全部改动,只要改变涉及到的那一部分的函数摘要即可。

基于动态规划
对于某些函数,可以记忆 Entry 抽象状态输入和 Exit 抽象输出的关系,然后下一次经过这个函数时,如果答案已知,就不必重新跑一遍了。但是也很明显,如果函数中的全局变量改变,那么结果就可能不太精确,这也体现了函数式编程在程序分析的优越性。更进一步,因为抽象状态如果分的比较细,那么就会更加精确,然而记忆输入输出映射的表将会非常大,读写开销会很大。而抽象状态分的比较粗,那么就会不精确。考虑到递归函数,那么递归过程中输入的值可能总是不一样。

例如上图就说明了粗粒度和细粒度两种方式,而且如果满足分配性的话,将会很有帮助。
再深入一些,假如采用加边的方式会出现不必要的分析,比如 C–>F 是不必要的,因为一般只要入口处到任意一个可达节点即可。但是 C 是不可达的。于是需要做一些改进,避免不需要的内部可达性计算。
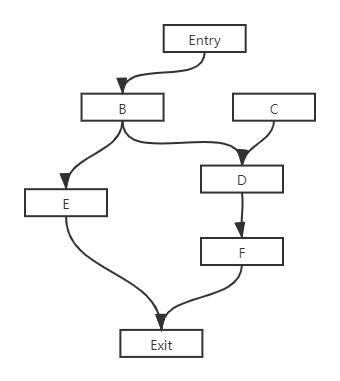
比较直观的想法如下,具体算法不细究:
- 尽量只从 entry 节点出发。
- 只有可达的内部节点有多条进来的路径,才复用。
基于函数摘要
首先明白为什么要采用函数摘要,它解决了什么问题。首先,根据分析的目标,函数内部的某些操作实际上是「相互抵消」的,如果能够对函数的性质进行抽象,提取摘要,那么就不用每一次都跑这个函数,减少状态转换的步骤。其次,库函数是非常多的,而且库函数功能完全是确定的,没有必要分析库函数内部代码,只需要库函数的摘要信息即可。所以如果节省下来的冗余计算大于摘要花费,则加速 了程序分析。基本思想是:
- 将一个过程摘要成一个转换函数。
- 库函数可以提前做成摘要,在分析用户代码的时 候直接使用摘要
具体到之前基于图的数据流分析,天然的契合了函数摘要的思想。因为图的可达性清晰的表示了每个函数的入口和出口的关系。

但是,由于每个变量都要从入口跑到出口,如果变量很多,那么边将会很复杂。考虑到效率因素,还需要进一步优化。
为了进一步优化,我们不生成那么庞大的图,而是沿控制流图合并转换函数,采用函数嵌套和合,用一个状态转换函数表达函数。
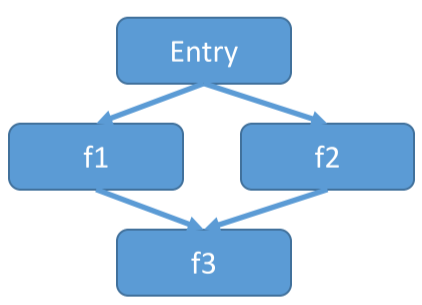
例如上图可以表示成
注意嵌套表达式的写法,为了避免嵌套,用右结合表示嵌套和合并:
我们继续研究,发现标准型合并和函数嵌套之后,仍然满足标准型,推导和结论见下图。

交汇的结果是,新生成的变量的并集,需要删除的变量是交集,可证明交汇之后的结果满足半格性质。最大元 Gen 为空集,KILL 为全集。而且可以证明,采用函数摘要之后的结果,一定会是 sound 的,而且和原来是等价的。(具体证明实在没看懂)。






