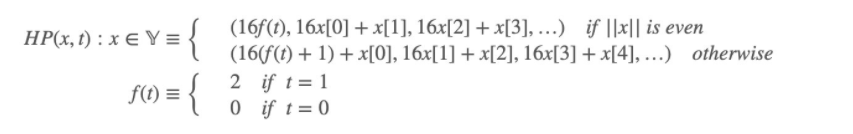1. 交易的签名
  2. 理解收据receipt
  3. 理解区块
  4. 理解交易
  5. blockchain核心
  6. forkId 解读
  7. 布隆过滤器原理
  8. oracle 原理和实现
  9. TxList 解读
  10. 交易池分析
  11. MPT树
  12. 区块同步
  13. geth源码学习——介绍
  14. How Geth starts its server

由于MPT 树不属于core部分所以有些地方并没有详细的解读，仅供参考。

由于该部分网上的解读都差异不大，故该文章大部分是进行整合，并且加上个人阅读源码的一些看法，所有图片都已经上传到个人仓库。

感谢前辈的精湛分析！

image-20220327222113848

前缀树 Trie

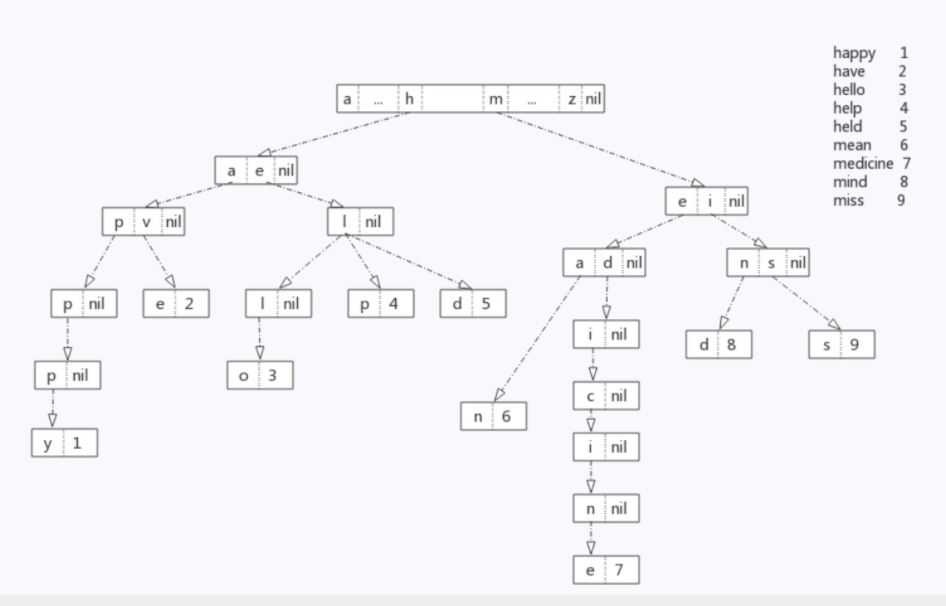
前缀树（又称字典树），通常来说，一个前缀树是用来存储字符串的。前缀树的每一个节点代表一个字符串（前缀）。每一个节点会有多个子节点，通往不同子节点的路径上有着不同的字符。子节点代表的字符串是由节点本身的原始字符串，以及通往该子节点路径上所有的字符组成的。如下图所示：

image-20220330161620588

Trie 的结点看上去是这样子的：

[ [Ia, Ib, … I*], value]

其中 [Ia, Ib, ... I*] 在本文中我们将其称为结点的 索引数组 ，它以 key 中的下一个字符为索引，每个元素I*指向对应的子结点。 value 则代表从根节点到当前结点的路径组成的 key 所对应的值。如果不存在这样一个 key，则 value 的值为空。

前缀树的性质：

  1. 每一层节点上面的值都不相同；
  2. 根节点不存储值；除根节点外每一个节点都只包含一个字符，代表的字符串是由节点本身的原始字符串，以及通往该子节点路径上所有的字符。
  3. 前缀树的查找效率是O(m)O(m)，mm为所查找节点的长度，而哈希表的查找效率为O(1)O(1)。且一次查找会有 m 次 IO开销，相比于直接查找，无论是速率、还是对磁盘的压力都比较大。
  4. 当存在一个节点，其内容很长（如一串很长的字符串），当树中没有与他相同前缀的分支时，为了存储该节点，需要创建许多非叶子节点来构建根节点到该节点间的路径，造成了存储空间的浪费。

压缩前缀树 Patricia Tree

基数树（也叫基数特里树或压缩前缀树）是一种数据结构，是一种更节省空间的前缀树，其中作为唯一子节点的每个节点都与其父节点合并，边既可以表示为元素序列又可以表示为单个元素。 因此每个内部节点的子节点数最多为基数树的基数 r ，其中 r 为正整数， x 为 2 的幂， x≥1 ，这使得基数树更适用于对于较小的集合（尤其是字符串很长的情况下）和有很长相同前缀的字符串集合。

  1. 示例 1：

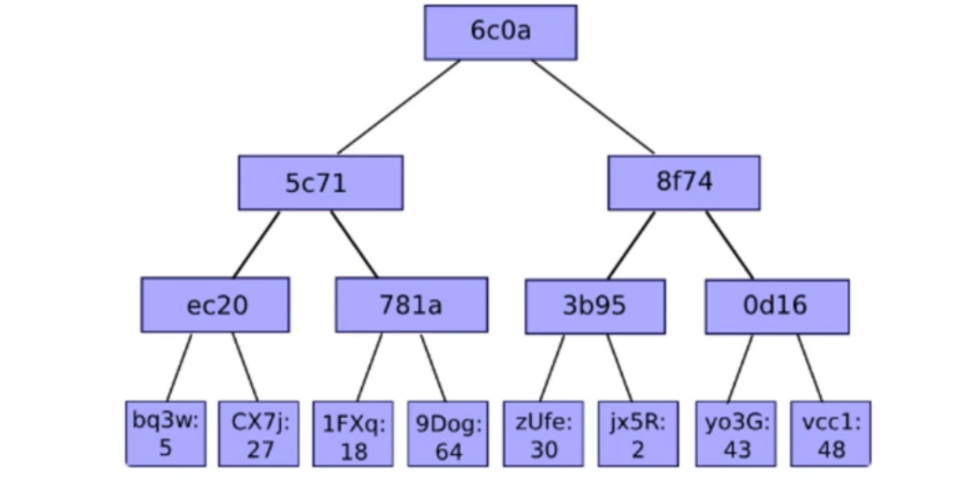
image-20220330162035687

图中可以很容易看出数中所存储的键值对：

  • 6c0a5c71ec20bq3w => 5
  • 6c0a5c71ec20CX7j => 27
  • 6c0a5c71781a1FXq=> 18
  • 6c0a5c71781a9Dog => 64
  • 6c0a8f743b95zUfe => 30
  • 6c0a8f743b95jx5R => 2
  • 6c0a8f740d16y03G => 43
  • 6c0a8f740d16vcc1 => 48
  1. 示例 2：

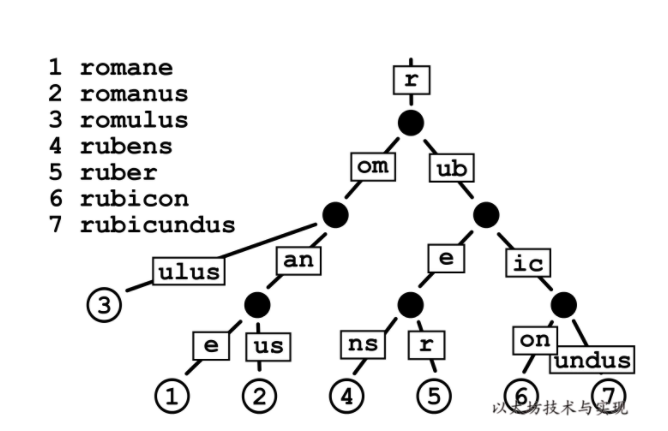
image-20220330162102535

虽然基数树使得以相同字符序列开头的键的值在树中靠得更近，但是它们可能效率很低。 例如，当你有一个超长键且没有其他键与之共享前缀时，即使路径上没有其他值，但你必须在树中移动（并存储）大量节点才能获得该值。 这种低效在以太坊中会更加明显，因为参与树构建的 Key 是一个哈希值有 64 长（32 字节），则树的最长深度是 64。树中每个节点必须存储 32 字节，一个 Key 就需要至少 2KB 来存储，其中包含大量空白内容。 因此，在经常需要更新的以太坊状态树中，优化改进基数树，以提高效率、降低树的深度和减少 IO 次数，是必要的。

默克尔树 Merkle Tree

Merkle树看起来非常像二叉树，其叶子节点上的值通常为数据块的哈希值，而非叶子节点上的值，所以有时候Merkle tree也表示为Hash tree，如下图所示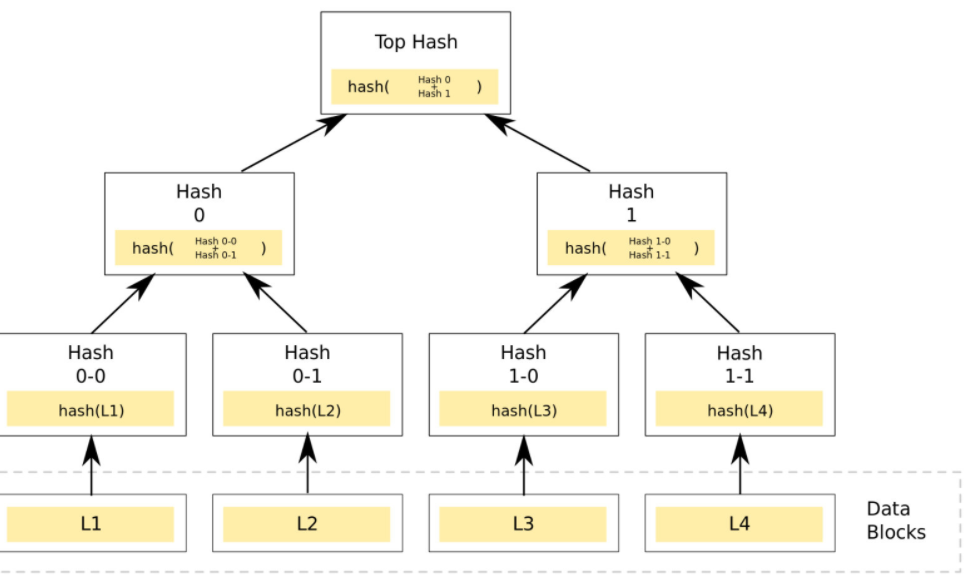：image-20220330162144911https://tva1.sinaimg.cn/large/0081Kckwgy1gm69qu5vh8j31ba0ragpn.jpg)

在构造Merkle树时，首先要计算数据块的哈希值，通常，选用SHA-256等哈希算法。但如果仅仅防止数据不是蓄意的损坏或篡改，可以改用一些安全性低(实际生活中CRC16基本达到 100%的正确率)但效率高的校验和算法，如CRC。然后将数据块计算的哈希值两两配对（如果是奇数个数，最后一个自己与自己配对），计算上一层哈希，再重复这个步骤，一直到计算出根哈希值。

所以我们可以简单总结出merkle Tree 有以下几个性质：

  • 校验整体数据的正确性
  • 快速定位错误
  • 快速校验部分数据是否在原始的数据中
  • 存储空间开销大（大量中间哈希）(显然对于以太坊很致命)

以太坊的改进方案

使用[]byte 作为 key 类型

在以太坊的 Trie 模块中，key 和 value 都是[]byte 类型。如果要使用其它类型，需要将其转换成[]byte 类型（比如使用rlp进行转换）。

Nibble ：是 key 的基本单元，是一个四元组（四个 bit 位的组合例如二进制表达的 0010 就是一个四元组）

在 Trie 模块对外提供的接口中，key 类型是[]byte。但在内部实现里，将 key 中的每个字节按高 4 位和低 4 位拆分成了两个字节。比如你传入的 key 是：

[0x1a, 0x2b, 0x3c, 0x4d]

Trie 内部将这个 key 拆分成：

[0x1, 0xa, 0x2, 0xb, 0x3, 0xc, 0x4, 0xd]

Trie 内部的编码中将拆分后的每一个字节称为 nibble

如果使用一个完整的 byte 作为 key 的最小单位，那么前文提到的索引数组的大小应该是 256（byte 作为数组的索引，最大值为 255，最小值为 0）（8 位282^8 )。而索引数组的每个元素都是一个 32 字节的哈希,这样每个结点要占用大量的空间。并且索引数组中的元素多数情况下是空的，不指向任何结点。因此这种实现方法占用大量空间而不使用。以太坊的改进方法，可以将索引数组的大小降为 16（4 个 bit 的最大值为 0xF，最小值为 0）(4 位242^4 ），因此大大减少空间的浪费。

新增类型节点

前缀树和 merkle 树存在明显的局限性，所以以太坊为 MPT 树新增了几种不同类型的树节点，通过针对不同节点不同操作来解决效率以及存储上的问题。

  1. 空白节点 ：简单的表示空，在代码中是一个空串;NULL

  2. 分支节点 ：分支节点有 17 个元素，回到 Nibble，四元组是 key 的基本单元，四元组最多有 16 个值。所以前 16 个必将落入到在其遍历中的键的十六个可能的半字节值中的每一个。第 17 个是存储那些在当前结点结束了的节点(例如， 有三个 key,分别是 (abc ,abd, ab) 第 17 个字段储存了 ab 节点的值) ;

    branch Node [0,1,…,16,value]

  3. 叶子节点：只有两个元素，分别为 key 和 value;

    leaf Node [key,value]

  4. 扩展节点 ：有两个元素，一个是 key 值，还有一个是 hash 值，这个 hash 值指向下一个节点;

    extension Node: [key,value]

此外，为了将 MPT 树存储到数据库中，同时还可以把 MPT 树从数据库中恢复出来，对于 Extension 和 Leaf 的节点类型做了特殊的定义：如果是一个扩展节点，那么前缀为 0，这个 0 加在 key 前面。如果是一个叶子节点，那么前缀就是 1。同时对key 的长度就奇偶类型也做了设定，如果是奇数长度则标示 1，如果是偶数长度则标示 0。

多种节点类型的不同操作方式，虽然提升了效率，但复杂度被加大。而在 geth 中，为了适应实现，节点类型的设计稍有不同：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//trie/node.go:35
type (
	fullNode struct { //分支节点
		Children [17]node
		flags    nodeFlag
	}
	shortNode struct { //短节点：叶子节点、扩展节点
		Key   []byte
		Val   node
		flags nodeFlag
	}
	hashNode  []byte //哈希节点
	valueNode []byte //数据节点,dui'ying值就是实际的数据值
)
var nilValueNode = valueNode(nil) //空白节点
  • fullNode: 分支节点，fullNode[16]的类型是 valueNode。前 16 个元素对应键中可能存在的一个十六进制字符。如果键[key,value]在对应的分支处结束，则在列表末尾存储 value 。
  • shortNode: 叶子节点或者扩展节点，当 shortNode.Key 的末尾字节是终止符 16 时表示为叶子节点。当 shortNode 是叶子节点是，Val 是 valueNode。
  • hashNode: 应该取名为 collapsedNode 折叠节点更合适些，但因为其值是一个哈希值当做指针使用，所以取名 hashNode。使用这个哈希值可以从数据库读取节点数据展开节点。
  • valueNode: 数据节点，实际的业务数据值，严格来说他不属于树中的节点，它只存在于 fullNode.Children 或者 shortNode.Val 中。

各类 Key

在改进过程中，为适应不同场景应用，以太坊定义了几种不同类型的 key 。

  1. keybytes ：数据的原始 key
  2. Secure Key: 是 Keccak256(keybytes) 结果，用于规避 key 深度攻击，长度固定为 32 字节。
  3. Hex Key: 将 Key 进行半字节拆解后的 key ，用于 MPT 的树路径中和降低子节点水平宽度。
  4. HP Key: Hex 前缀编码(hex prefix encoding)，在节点存持久化时，将对节点 key 进行压缩编码，并加入节点类型标签，以便从存储读取节点数据后可分辨节点类型。

下图是 key 有特定的使用场景，基本支持逆向编码，在下面的讲解中 Key 在不同语义下特指的类型有所不同

节点结构改进

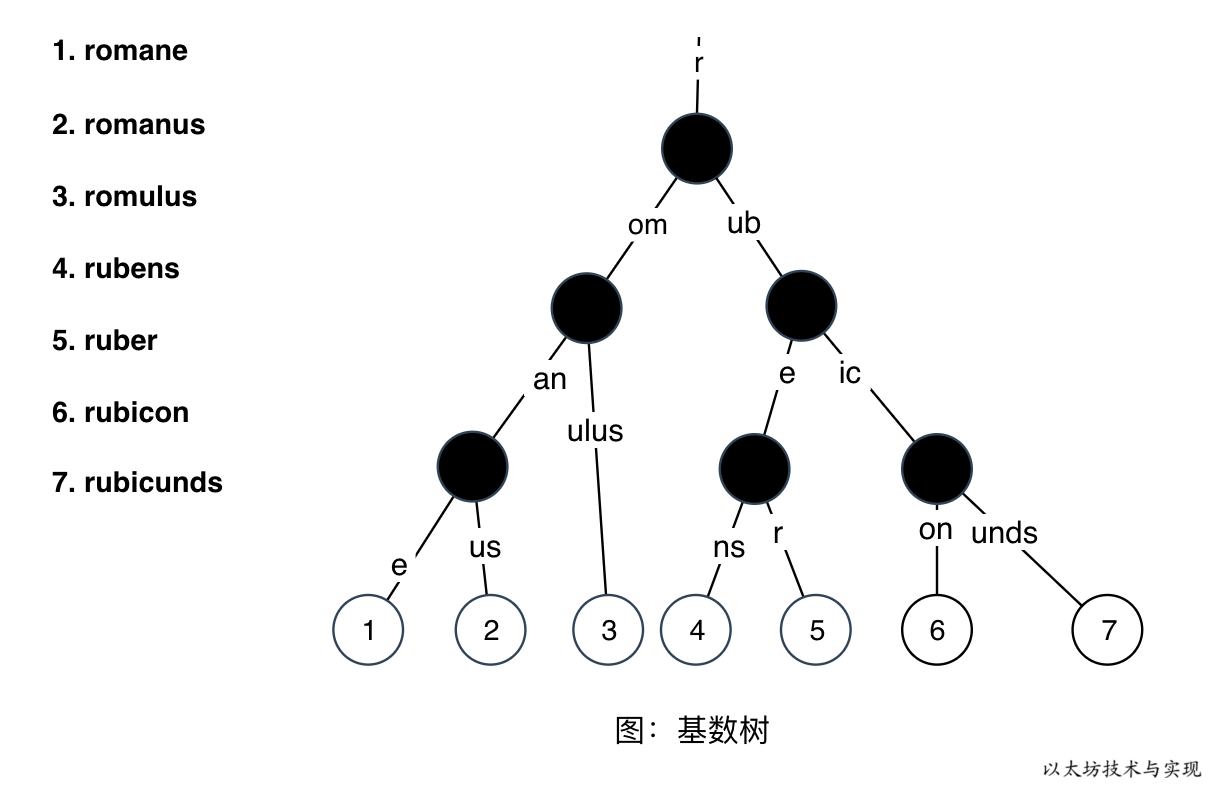
当我们把一组数据（romane、romanus、romulus、rubens、ruber、rubicon、rubicunds）写入基数树中时，得到如下一颗基数树：

img

在上图的基数树中，持久化节点，有 12 次 IO。数据越多时，节点数越多，IO 次数越多。另外当树很深时，可能需要遍历到树的底部才能查询到数据。 面对此效率问题，以太坊在树中加入了一种名为分支节点(branch node) 的节点结构，将其子节点直接包含在自身的数据插槽中。

这样可缩减树深度和减少 IO 次数，特别是当插槽中均有子节点存在时，改进效果越明显。 下图是上方基数树在采用分支节点后的树节点逻辑布局：

img

从图中可以看出节点数量并无改进，仅仅是改变了节点的存放位置，节点的分布变得紧凑。图中大黑圆圈均为分支节点，它包含一个或多个子节点， 这降低了 IO 和查询次数，在上图中，持久化 IO 只有 6 次，低于基数树的 12 次。

这是因为在持久化分支节点时，并不是将叶子节点分开持久化，而是将其存储在一块。并将持久化内容的哈希值作为一个新节点来参与树的进一步持久化，这种新型的节点称之为扩展节点。比如，数据 rubicon(6) 和 rubicunds(7) 是被一起持久化，在查询数据 rubicon 时，将根据 hasNode 值从数据库中读取分支节点内容，并解码成分支节点，内含 rubicon 和 rubicunds。

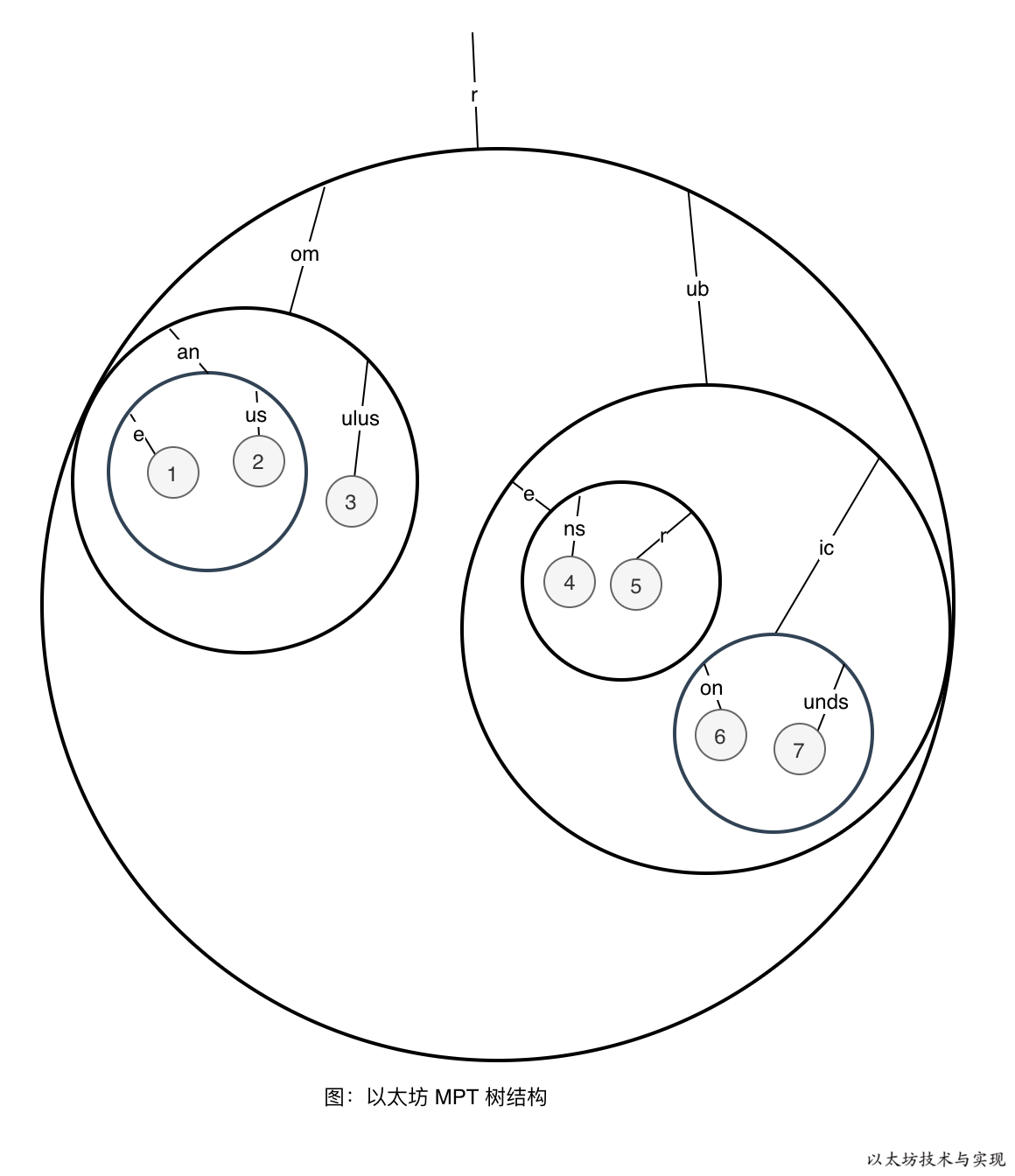
另外一个可以参考的官方图：

image-20220327222113848

另外，数据 Key 在进入 MPT 前已转换 Secure Key。 因此，key 长度为 32 字节，每个字节的值范围是[0 - 255]。 如果在分支节点中使用 256 个插槽，空间开销非常高，造成浪费，毕竟空插槽在持久化时也需要占用空间。同时超大容量的插槽，也会可能使得持久化数据过大，可能会造成读取持久化数据时占用过多内存。 如果将 Key 进行Hex 编码，每个字节值范围被缩小到 [0-15] 内(4bits)。这样，分支节点只需要 16 个插槽来存放子节点。

上图中 0 - f 插槽索引是半字节值，也是 Key 路径的一部分。虽然一定程度上增加了树高，但降低了分支节点的存储大小，也保证了一定的分支节点合并量。

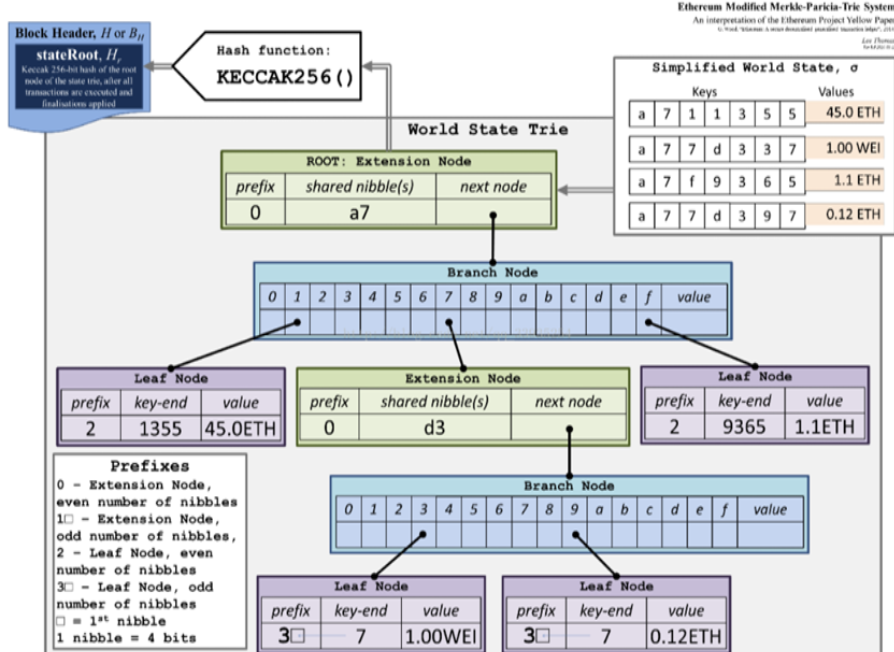
以太坊中使用到的 MPT 树结构

  • State Trie区块头中的状态树
    • key => sha3(以太坊账户地址 address)
    • value => rlp(账号内容信息 account)
  • Transactions Trie 区块头中的交易树
    • key => rlp(交易的偏移量 transaction index)
    • 每个块都有各自的交易树，且不可更改
  • Receipts Trie区块头中的收据树
    • key = rlp(交易的偏移量 transaction index)
    • 每个块都有各自的回执树，且不可更改
  • Storage Trie存储树
    • 存储只能合约状态
    • 每个账号有自己的 Storage Trie

这两个区块头中，state root、tx root、 receipt root分别存储了这三棵树的树根，第二个区块显示了当账号 17 5 的数据变更(27 -> 45)的时候，只需要存储跟这个账号相关的部分数据，而且老的区块中的数据还是可以正常访问。

key 编码规则

三种编码方式分别为：

  1. Raw编码（原生的字符）；
  2. Hex编码（扩展的 16 进制编码）；
  3. Hex-Prefix编码（16 进制前缀编码）；

Raw 编码

Raw编码就是原生的key值，不做任何改变。这种编码方式的key，是MPT对外提供接口的默认编码方式。

例如一条 key 为“cat”，value 为“dog”的数据项，其 Raw 编码就是[‘c’, ‘a’, ‘t’]，换成 ASCII 表示方式就是[63, 61, 74]

Hex 编码

Hex 编码用于对内存中 MPT 树节点 key 进行编码.

为了减少分支节点孩子的个数，将数据 key 进行半字节拆解而成。即依次将 key[0],key[1],…,key[n] 分别进行半字节拆分成两个数，再依次存放在长度为 len(key)+1 的数组中。 并在数组末尾写入终止符 16。算法如下：

半字节，在计算机中，通常将 8 位二进制数称为字节，而把 4 位二进制数称为半字节。 高四位和低四位，这里的“位”是针对二进制来说的。比如数字 250 的二进制数为 11111010，则高四位是左边的 1111，低四位是右边的 1010。

从Raw编码向Hex编码的转换规则是：

  • Raw编码输入的每个字符分解为高 4 位和低 4 位
  • 如果是叶子节点，则在最后加上Hex值0x10表示结束
  • 如果是扩展节点不附加任何Hex值

例如：字符串 “romane” 的 bytes 是 [114 111 109 97 110 101]，在 HEX 编码时将其依次处理：

i key[i] key[i]二进制 nibbles[i*2]=高四位 nibbles[i*2+1]=低四位
0 114 01110010 0111= 7 0010= 2
1 111 01101111 0110=6 1111=15
2 109 01101101 0110=6 1101=13
3 97 01100001 0110=6 0001=1
4 110 01101110 0110=6 1110=14
5 101 01100101 0110=6 0101=5

最终得到 Hex(“romane”) = [7 2 6 15 6 13 6 1 6 14 6 5 16]

1
2
3
4
5
6
7
8
9
10
11
// 源码实现
func keybytesToHex(str []byte) []byte {
	l := len(str)*2 + 1
	var nibbles = make([]byte, l)
	for i, b := range str {
		nibbles[i*2] = b / 16   // 高四位
		nibbles[i*2+1] = b % 16 // 低四位
	}
	nibbles[l-1] = 16 // 最后一位存入标示符 代表是hex编码
	return nibbles
}

这里解释一下为啥 不处理叶子节点和扩展结点的区别，而是直接采用nibbles[l-1]=16，因为扩展节点不储存字符串信息，所以说字符串转换的时候直接按叶子节点处理即可，但是Hex=>Hex Prefix的时候要考虑是不是扩展结点的问题；

Hex-Prefix编码

数学公式定义：

image-20220330161849571

Hex-Prefix 编码是一种任意量的半字节转换为数组的有效方式，还可以在存入一个标识符来区分不同节点类型。 因此 HP 编码是在由一个标识符前缀和半字节转换为数组的两部分组成。存入到数据库中存在节点 Key 的只有扩展节点和叶子节点，因此 HP 只用于区分扩展节点和叶子节点，不涉及无节点 key 的分支节点。其编码规则如下图：

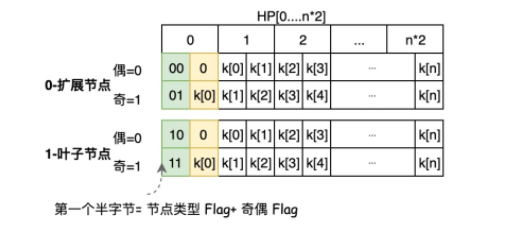
image-20220330162436055

前缀标识符由两部分组成：节点类型和奇偶标识，并存储在编码后字节的第一个半字节中。 0 表示扩展节点类型，1 表示叶子节点，偶为 0，奇为 1。最终可以得到唯一标识的前缀标识：

  • 0：偶长度的扩展节点
  • 1：奇长度的扩展节点
  • 2：偶长度的叶子节点
  • 3：奇长度的叶子节点

当偶长度时，第一个字节的低四位用0填充，当是奇长度时，则将 key[0] 存放在第一个字节的低四位中，这样 HP 编码结果始终是偶长度。 这里为什么要区分节点 key 长度的奇偶呢？这是因为，半字节 1 和 01 在转换为 bytes 格式时都成为<01>，无法区分两者。

例如，上图 “以太坊 MPT 树的哈希计算”中的控制节点 1 的 key 为 [ 7 2 6 f 6 d]，因为是偶长度，则 HP[0]= (00000000) =0，H[1:]= 解码半字节(key)。 而节点 3 的 key 为 [1 6 e 6 5]，为奇长度，则 HP[0]= (0001 0001)=17。

HP编码的规则如下：

  • key 结尾为0x10，则去掉这个终止符
  • key 之前补一个四元组这个 Byte 第 0 位区分奇偶信息，第 1 位区分节点类型
  • 如果输入key的长度是偶数，则再添加一个四元组 0x0 在 flag 四元组后
  • 将原来的 key 内容压缩，将分离的两个 byte 以高四位低四位进行合并

十六进制前缀编码相当于一个逆向的过程，比如输入的是[6 2 6 15 6 2 16]，

根据第一个规则去掉终止符 16。根据第二个规则 key 前补一个四元组，从右往左第一位为 1 表示叶子节点，

从右往左第 0 位如果后面 key 的长度为偶数设置为 0，奇数长度设置为 1，那么四元组 0010 就是 2。

根据第三个规则，添加一个全 0 的补在后面，那么就是 20.根据第三个规则内容压缩合并，那么结果就是[0x20 0x62 0x6f 0x62]

HP 编码源码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
func hexToCompact(hex []byte) []byte {
	terminator := byte(0) //初始化一个值为0的byte，它就是我们上面公式中提到的t
	if hasTerm(hex) {     //验证hex是否有后缀编码，
		terminator = 1         //hex编码有后缀，证明是叶子节点，则t=1
		hex = hex[:len(hex)-1] //此处只是去掉后缀部分的hex编码
	}
	//Compact开辟的空间长度为hex编码的一半再加1，这个1对应的空间是Compact的前缀
	buf := make([]byte, len(hex)/2+1)
	////这一阶段的buf[0]可以理解为公式中的16*f(t)
    //判断节点类型
	buf[0] = terminator << 5 // the flag byte
    //判断jiou
	if len(hex)&1 == 1 {     //hex 长度为奇数，则逻辑上说明hex有前缀
		buf[0] |= 1 << 4 ////这一阶段的buf[0]可以理解为公式中的16*（f(t)+1）
		buf[0] |= hex[0] // first nibble is contained in the first byte
		hex = hex[1:]    //此时获取的hex编码无前缀无后缀
	}
	decodeNibbles(hex, buf[1:]) //将hex编码映射到compact编码中
	return buf                  //返回compact编码
}

//compact编码转化为Hex编码
func compactToHex(compact []byte) []byte {
	if len(compact) == 0 {
		return compact
	}
	//进行展开即可
	base := keybytesToHex(compact)

	// apply terminator flag
	// base[0]包括四种情况
	// 00000000 扩展节点偶数位
	// 00000001 扩展节点奇数位
	// 00000010 叶子节点偶数位
	// 00000011 叶子节点奇数位

	// delete terminator flag
	if base[0] < 2 { //扩展结点
		base = base[:len(base)-1]
	}
	// apply odd flag
	//如果是偶数位，chop等于2，否则等于1
	chop := 2 - base[0]&1
	return base[chop:]
}
// 将keybytes 转成十六进制
func keybytesToHex(str []byte) []byte {
    l := len(str)*2 + 1
     //将一个keybyte转化成两个字节
    var nibbles = make([]byte, l)
    for i, b := range str {
        nibbles[i*2] = b / 16
        nibbles[i*2+1] = b % 16
    }
    //末尾加入Hex标志位16
    nibbles[l-1] = 16
    return nibbles
}

// 将十六进制的bibbles转成key bytes，这只能用于偶数长度的key
func hexToKeybytes(hex []byte) []byte {
    if hasTerm(hex) {
        hex = hex[:len(hex)-1]
    }
    if len(hex)&1 != 0 {
        panic("can't convert hex key of odd length")
    }
    key := make([]byte, (len(hex)+1)/2)
    decodeNibbles(hex, key)
    return key
}

func decodeNibbles(nibbles []byte, bytes []byte) {
    for bi, ni := 0, 0; ni < len(nibbles); bi, ni = bi+1, ni+2 {
        bytes[bi] = nibbles[ni]<<4 | nibbles[ni+1]
    }
}

// 返回a和b的公共前缀的长度
func prefixLen(a, b []byte) int {
    var i, length = 0, len(a)
    if len(b) < length {
        length = len(b)
    }
    for ; i < length; i++ {
        if a[i] != b[i] {
            break
        }
    }
    return i
}

// 十六进制key是否有结束标志符
func hasTerm(s []byte) bool {
    return len(s) > 0 && s[len(s)-1] == 16
}

以上三种编码方式的转换关系为：

  • Raw 编码：原生的 key 编码，是 MPT 对外提供接口中使用的编码方式，当数据项被插入到树中时，Raw 编码被转换成 Hex编码**；
  • Hex 编码：16 进制扩展编码，用于对内存中树节点 key 进行编码，当树节点被持久化到数据库时，Hex 编码被转换成 HP 编码；
  • HP 编码：16 进制前缀编码，用于对数据库中树节点 key 进行编码，当树节点被加载到内存时，HP 编码被转换成 Hex 编码；

如下图：

image-20220330161823864

以上介绍的 MPT 树，可以用来存储内容为任何长度的key-value数据项。倘若数据项的key长度没有限制时，当树中维护的数据量较大时，仍然会造成整棵树的深度变得越来越深，会造成以下影响：

  • 查询一个节点可能会需要许多次 IO 读取，效率低下；
  • 系统易遭受 Dos 攻击，攻击者可以通过在合约中存储特定的数据，“构造”一棵拥有一条很长路径的树，然后不断地调用SLOAD指令读取该树节点的内容，造成系统执行效率极度下降；
  • 所有的 key 其实是一种明文的形式进行存储；

为了解决以上问题，以太坊对MPT再进行了一次封装，对数据项的key进行了一次哈希计算，因此最终作为参数传入到 MPT 接口的数据项其实是(sha3(key), value)

优势：

  • 传入 MPT 接口的 key 是固定长度的（32 字节），可以避免出现树中出现长度很长的路径；

劣势：

  • 每次树操作需要增加一次哈希计算；
  • 需要在数据库中存储额外的sha3(key)与key之间的对应关系；

完整的编码流程如图：

image-20220330162503765

MPT 轻节点

上面的 MPT 树，有两个问题：

  • 每个节点都包含有大量信息，并且叶子节点中还包含有完整的数据信息。如果该 MPT 树并没有发生任何变化，并且没有被使用，则会白白占用一大片空间，想象一个以太坊，有多少个 MPT 树，都在内存中，那还了得。
  • 并不是任何的客户端都对所有的 MPT 树都感兴趣，若每次都把完整的节点信息都下载下，下载时间长不说，并且会占用大量的磁盘空间。

解决方式

为了解决上述问题，以太坊使用了一种缓存机制，可以称为是轻节点机制，大体如下：

  • 若某节点数据一直没有发生变化，则仅仅保留该节点的 32 位 hash 值，剩下的内容全部释放
  • 若需要插入或者删除某节点，先通过该 hash 值 db 中查找对应的节点，并加载到内存，之后再进行删除插入操作

轻节点中添加数据

内存中只有这么一个轻节点，但是我要添加一个数据，也就是要给完整的 MPT 树中添加一个叶子节点，怎么添加？大体如下图所示：

image-20210101204824090

以上主要介绍了以太坊中的 MPT 树的原理，这篇主要会对 MPT 树涉及的源码进行拆解分析。trie模块主要有以下几个文件：

1
2
3
4
5
6
7
8
9
|-encoding.go 主要讲编码之间的转换
|-hasher.go 实现了从某个结点开始计算子树的哈希的功能
|-node.go 定义了一个Trie树中所有结点的类型和解析的代码
|-sync.go 实现了SyncTrie对象的定义和所有方法
|-iterator.go 定义了所有枚举相关接口和实现
|-secure_trie.go 实现了SecureTrie对象
|-proof.go 为key构造一个merkle证明
|-trie.go Trie树的增删改查
|-database.go 对内存中的trie树节点进行引用计数

实现概览

encoding.go

这个主要是讲三种编码（KEYBYTES encoding、HEX encoding、COMPACT encoding）的实现与转换，trie中全程都需要用到这些，该文件中主要实现了如下功能：

  1. hex 编码转换为 Compact 编码：hexToCompact()
  2. Compact 编码转换为 hex 编码：compactToHex()
  3. keybytes 编码转换为 Hex 编码：keybytesToHex()
  4. hex 编码转换为 keybytes 编码：hexToKeybytes()
  5. 获取两个字节数组的公共前缀的长度：prefixLen()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
func hexToCompact(hex []byte) []byte {
    terminator := byte(0)
    if hasTerm(hex) { //检查是否有结尾为0x10 => 16
        terminator = 1 //有结束标记16说明是叶子节点
        hex = hex[:len(hex)-1] //去除尾部标记
    }
    buf := make([]byte, len(hex)/2+1) // 字节数组

    buf[0] = terminator << 5 // 标志byte为00000000或者00100000
    //如果长度为奇数，添加奇数位标志1，并把第一个nibble字节放入buf[0]的低四位
    if len(hex)&1 == 1 {
        buf[0] |= 1 << 4 // 奇数标志 00110000
        buf[0] |= hex[0] // 第一个nibble包含在第一个字节中 0011xxxx
        hex = hex[1:]
    }
    //将两个nibble字节合并成一个字节
    decodeNibbles(hex, buf[1:])
    return buf

//compact编码转化为Hex编码
func compactToHex(compact []byte) []byte {
    base := keybytesToHex(compact)
    base = base[:len(base)-1]
     // apply terminator flag
    // base[0]包括四种情况
    // 00000000 扩展节点偶数位
    // 00000001 扩展节点奇数位
    // 00000010 叶子节点偶数位
    // 00000011 叶子节点奇数位

    // apply terminator flag
    if base[0] >= 2 {
       //如果是叶子节点，末尾添加Hex标志位16
        base = append(base, 16)
    }
    // apply odd flag
    //如果是偶数位，chop等于2，否则等于1
    chop := 2 - base[0]&1
    return base[chop:]
}
//compact编码转化为Hex编码
func compactToHex(compact []byte) []byte {
    base := keybytesToHex(compact)
    base = base[:len(base)-1]
     // apply terminator flag
    // base[0]包括四种情况
    // 00000000 扩展节点偶数位
    // 00000001 扩展节点奇数位
    // 00000010 叶子节点偶数位
    // 00000011 叶子节点奇数位

    // apply terminator flag
    if base[0] >= 2 {
       //如果是叶子节点，末尾添加Hex标志位16
        base = append(base, 16)
    }
    // apply odd flag
    //如果是偶数位，chop等于2，否则等于1
    chop := 2 - base[0]&1
    return base[chop:]
}
// 将十六进制的bibbles转成key bytes，这只能用于偶数长度的key
func hexToKeybytes(hex []byte) []byte {
    if hasTerm(hex) {
        hex = hex[:len(hex)-1]
    }
    if len(hex)&1 != 0 {
        panic("can't convert hex key of odd length")
    }
    key := make([]byte, (len(hex)+1)/2)
    decodeNibbles(hex, key)
    return key
}
// 返回a和b的公共前缀的长度
func prefixLen(a, b []byte) int {
    var i, length = 0, len(a)
    if len(b) < length {
        length = len(b)
    }
    for ; i < length; i++ {
        if a[i] != b[i] {
            break
        }
    }
    return i
}

node.go

node 接口分四种实现: fullNode，shortNode，valueNode，hashNode，其中只有 fullNode 和 shortNode 可以带有子节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
type (
	fullNode struct {
		Children [17]node // 分支节点
		flags    nodeFlag
	}
	shortNode struct { //扩展节点
		Key   []byte
		Val   node //可能指向叶子节点，也可能指向分支节点。
		flags nodeFlag
	}
	hashNode  []byte
	valueNode []byte // 叶子节点值，但是该叶子节点最终还是会包装在shortNode中
)

trie.go

Trie 对象实现了 MPT 树的所有功能，包括(key, value)对的增删改查、计算默克尔哈希，以及将整个树写入数据库中。

iterator.go

nodeIterator提供了遍历树内部所有结点的功能。其结构如下：此结构体是在trie.go定义的

1
2
3
4
5
type nodeIterator struct {
	trie.NodeIterator
	t   *odrTrie
	err error
}

里面包含了一个接口NodeIterator，它的实现则是由iterator.go来提供的，其方法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
func (it *nodeIterator) Next(descend bool) bool
func (it *nodeIterator) Hash() common.Hash
func (it *nodeIterator) Parent() common.Hash
func (it *nodeIterator) Leaf() bool
func (it *nodeIterator) LeafKey() []byte
func (it *nodeIterator) LeafBlob() []byte
func (it *nodeIterator) LeafProof() [][]byte
func (it *nodeIterator) Path() []byte {}
func (it *nodeIterator) seek(prefix []byte) error
func (it *nodeIterator) peek(descend bool) (*nodeIteratorState, *int, []byte, error)
func (it *nodeIterator) nextChild(parent *nodeIteratorState, ancestor common.Hash) (*nodeIteratorState, []byte, bool)
func (it *nodeIterator) push(state *nodeIteratorState, parentIndex *int, path []byte)
func (it *nodeIterator) pop()

NodeIterator的核心是Next方法，每调用一次这个方法，NodeIterator 对象代表的当前节点就会更新至下一个节点，当所有结点遍历结束，Next方法返回false。

生成 NodeIterator 接口的方法有以下 3 种：

①：Trie.NodeIterator(start []byte)

通过start参数指定从哪个路径开始遍历，如果为nil则从头到尾按顺序遍历。

②：NewDifferenceIterator(a, b NodeIterator)

当调用NewDifferenceIterator(a, b NodeIterator)后，生成的NodeIterator只遍历存在于 b 但不存在于 a 中的结点。

③：NewUnionIterator(iters []NodeIterator)

当调用NewUnionIterator(its []NodeIterator)后，生成的NodeIterator遍历的结点是所有传入的结点的合集。

database.go

Database是trie模块对真正数据库的缓存层，其目的是对缓存的节点进行引用计数，从而实现区块的修剪功能。主要方法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func NewDatabase(diskdb ethdb.KeyValueStore) *Database
func NewDatabaseWithCache(diskdb ethdb.KeyValueStore, cache int) *Database
func (db *Database) DiskDB() ethdb.KeyValueReader
func (db *Database) InsertBlob(hash common.Hash, blob []byte)
func (db *Database) insert(hash common.Hash, blob []byte, node node)
func (db *Database) insertPreimage(hash common.Hash, preimage []byte)
func (db *Database) node(hash common.Hash) node
func (db *Database) Node(hash common.Hash) ([]byte, error)
func (db *Database) preimage(hash common.Hash) ([]byte, error)
func (db *Database) secureKey(key []byte) []byte
func (db *Database) Nodes() []common.Hash
func (db *Database) Reference(child common.Hash, parent common.Hash)
func (db *Database) Dereference(root common.Hash)
func (db *Database) dereference(child common.Hash, parent common.Hash)
func (db *Database) Cap(limit common.StorageSize) error
func (db *Database) Commit(node common.Hash, report bool) error

security_trie.go

可以理解为加密了的trie的实现，ecurity_trie包装了一下trie树， 所有的key都转换成keccak256算法计算的hash值。同时在数据库里面存储hash值对应的原始的key。
但是官方在代码里也注释了，这个代码不稳定，除了测试用例，别的地方并没有使用该代码。

proof.go

  • Prove()：根据给定的key，在trie中，将满足key中最大长度前缀的路径上的节点都加入到proofDb（队列中每个元素满足：未编码的 hash 以及对应rlp编码后的节点）
  • VerifyProof()：验证proffDb中是否存在满足输入的hash，和对应 key 的节点，如果满足，则返回rlp解码后的该节点。

实现细节

①：Trie 树的初始化

如果root不为空，就通过resolveHash来加载整个Trie树，如果为空，就新建一个Trie树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func New(root common.Hash, db *Database) (*Trie, error) {
	if db == nil {
		panic("trie.New called without a database")
	}
	trie := &Trie{
		db: db,
	}
	if root != (common.Hash{}) && root != emptyRoot {
		rootnode, err := trie.resolveHash(root[:], nil)
		if err != nil {
			return nil, err
		}
		trie.root = rootnode
	}
	return trie, nil
}

②：Trie 树的插入

首先 Trie 树的插入是个递归调用的过程，它会从根开始找，一直找到合适的位置插入。

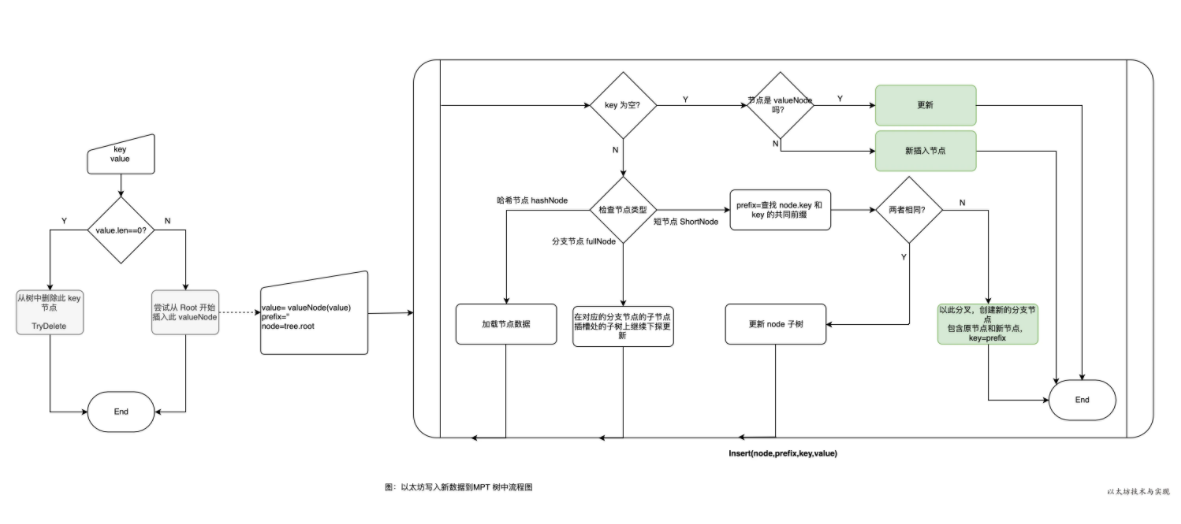
image-20220330162606450 
1
func (t *Trie) insert(n node, prefix, key []byte, value node) (bool, node, error)

参数说明：

  • n: 当前要插入的节点
  • prefix: 当前已经处理完的key(节点共有的前缀)
  • key: 未处理完的部分key，完整的key = prefix + key
  • value：需要插入的值

返回值说明：

  • bool : 操作是否改变了Trie树(dirty)
  • Node :插入完成后的子树的根节点

接下来就是分别对shortNode、fullNode、hashNode、nil 几种情况进行说明。

2.1：节点为 nil

空树直接返回shortNode， 此时整颗树的根就含有了一个shortNode节点。

1
2
case nil:
		return true, &shortNode{key, value, t.newFlag()}, nil

2.2 ：节点为 shortNode

  • 首先计算公共前缀，如果公共前缀就等于key，那么说明这两个key是一样的，如果value也一样的(dirty == false)，那么返回错误。
  • 如果没有错误就更新shortNode的值然后返回
  • 如果公共前缀不完全匹配，那么就需要把公共前缀提取出来形成一个独立的节点(扩展节点),扩展节点后面连接一个branch节点，branch节点后面看情况连接两个short节点。
  • 首先构建一个 branch 节点(branch := &fullNode{flags: t.newFlag()}),然后再 branch 节点的 Children 位置调用 t.insert 插入剩下的两个 short 节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
matchlen := prefixLen(key, n.Key)
		if matchlen == len(n.Key) {
			dirty, nn, err := t.insert(n.Val, append(prefix, key[:matchlen]...), key[matchlen:], value)
			if !dirty || err != nil {
				return false, n, err
			}
			return true, &shortNode{n.Key, nn, t.newFlag()}, nil
		}
		branch := &fullNode{flags: t.newFlag()}
		var err error
		_, branch.Children[n.Key[matchlen]], err = t.insert(nil, append(prefix, n.Key[:matchlen+1]...), n.Key[matchlen+1:], n.Val)
		if err != nil {
			return false, nil, err
		}
		_, branch.Children[key[matchlen]], err = t.insert(nil, append(prefix, key[:matchlen+1]...), key[matchlen+1:], value)
		if err != nil {
			return false, nil, err
		}
		if matchlen == 0 {
			return true, branch, nil
    }
		return true, &shortNode{key[:matchlen], branch, t.newFlag()}, nil

2.3: 节点为 fullNode

节点是fullNode(也就是分支节点)，那么直接往对应的孩子节点调用insert方法,然后把对应的孩子节点指向新生成的节点。

1
2
3
4
5
6
7
8
dirty, nn, err := t.insert(n.Children[key[0]], append(prefix, key[0]), key[1:], value)
		if !dirty || err != nil {
			return false, n, err
		}
		n = n.copy()
		n.flags = t.newFlag()
		n.Children[key[0]] = nn
		return true, n, nil

2.4: 节点为 hashnode

暂时还在数据库中的节点，先调用 t.resolveHash(n, prefix)来加载到内存，然后调用insert方法来插入。

1
2
3
4
5
6
7
8
9
rn, err := t.resolveHash(n, prefix)
		if err != nil {
			return false, nil, err
		}
		dirty, nn, err := t.insert(rn, prefix, key, value)
		if !dirty || err != nil {
			return false, rn, err
		}
		return true, nn, nil

③：Trie 树查询值

其实就是根据输入的hash，找到对应的叶子节点的数据。主要看TryGet方法。

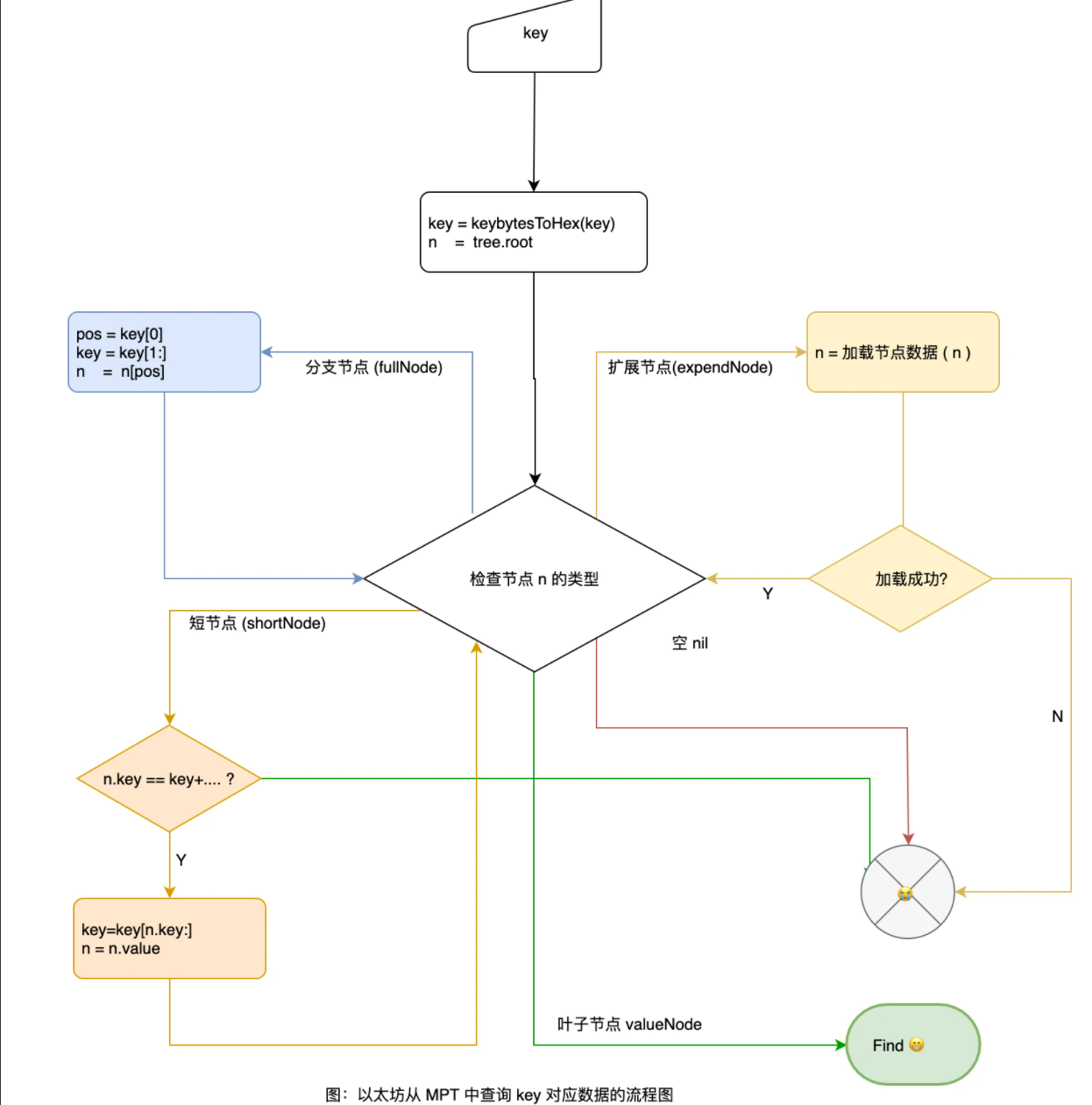
image-20220330162644392

参数：

  • origNode：当前查找的起始node位置
  • key：输入要查找的数据的hash
  • pos：当前hash匹配到第几位
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func (t *Trie) tryGet(origNode node, key []byte, pos int) (value []byte, newnode node, didResolve bool, err error) {
	switch n := (origNode).(type) {
	case nil: //表示当前trie是空树
		return nil, nil, false, nil
	case valueNode: ////这就是我们要查找的叶子节点对应的数据
		return n, n, false, nil
	case *shortNode: ////在叶子节点或者扩展节点匹配
		if len(key)-pos < len(n.Key) || !bytes.Equal(n.Key, key[pos:pos+len(n.Key)]) {
			return nil, n, false, nil
		}
		value, newnode, didResolve, err = t.tryGet(n.Val, key, pos+len(n.Key))
		if err == nil && didResolve {
			n = n.copy()
			n.Val = newnode
		}
		return value, n, didResolve, err
	case *fullNode://在分支节点匹配
		value, newnode, didResolve, err = t.tryGet(n.Children[key[pos]], key, pos+1)
		if err == nil && didResolve {
			n = n.copy()
			n.Children[key[pos]] = newnode
		}
		return value, n, didResolve, err
	case hashNode: //说明当前节点是轻节点，需要从db中获取
		child, err := t.resolveHash(n, key[:pos])
		if err != nil {
			return nil, n, true, err
		}
		value, newnode, _, err := t.tryGet(child, key, pos)
		return value, newnode, true, err
...
}

didResolve用于判断trie树是否会发生变化，tryGet()只是用来获取数据的，当hashNode去db中获取该node值后需要更新现有的 trie，didResolve就会发生变化。其他就是基本的递归查找树操作。

删除数据

从 MPT 中删除数据节点，这比插入数据更加复杂。从树中删除一个节点是容易的，但在 MPT 中删除节点后需要根据前面的改进方案调整结构。 比如，原本是一个分支节点下有两个子节点，现在删除一个子节点后，只有一个子节点的分支节点的存储是无意义的，需要移除并将剩余的子节点上移。 下图是 MPT 中删除数据的流程图。

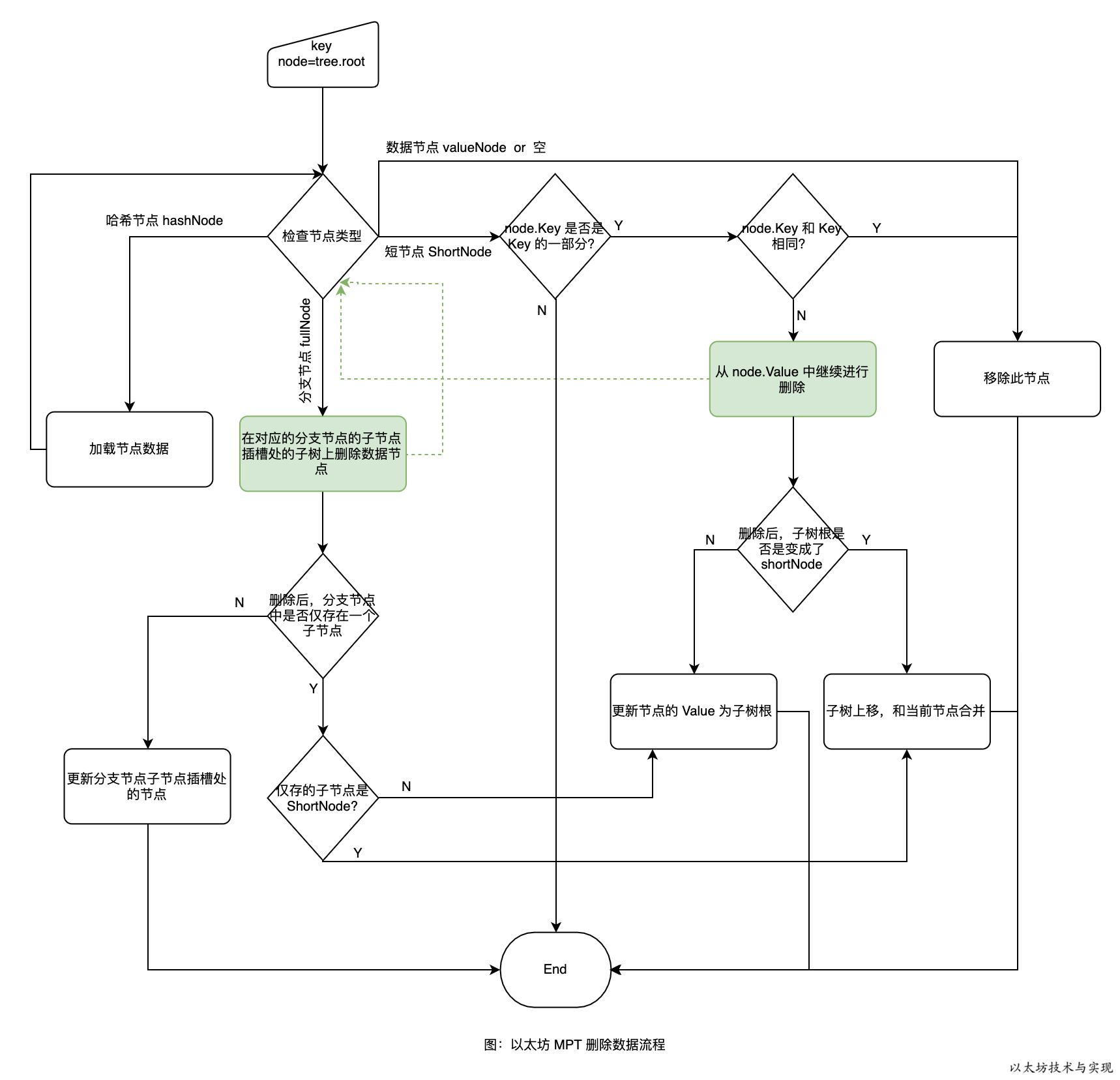以太坊技术与实现-图- MPT中删除数据的流程图同样，删除数据也是深度递归遍历。先深度查找，抵达数据应处位置，再从下向上依次更新此路径上的节点。 在删除过程中，主要是对删除后节点的调整。有两个原则：

  1. 分支节点至少要有两个子节点，如果只有一个子节点或者没有则需要调整。
  2. shortNode 的 value 是 shortNode 时可合并。

删除数据也涉及路径上节点的更新，图中的绿色虚线是表示递归删除节点。

树更新实例

下面，我演示依次将一组数据 romane、romanus、romulus、rubens、ruber、rubicon、rubicunds 插入到 MPT 中时的树结构的变化情况。

首先依次写入：romane、romanus、romulus 后树的变化如下：

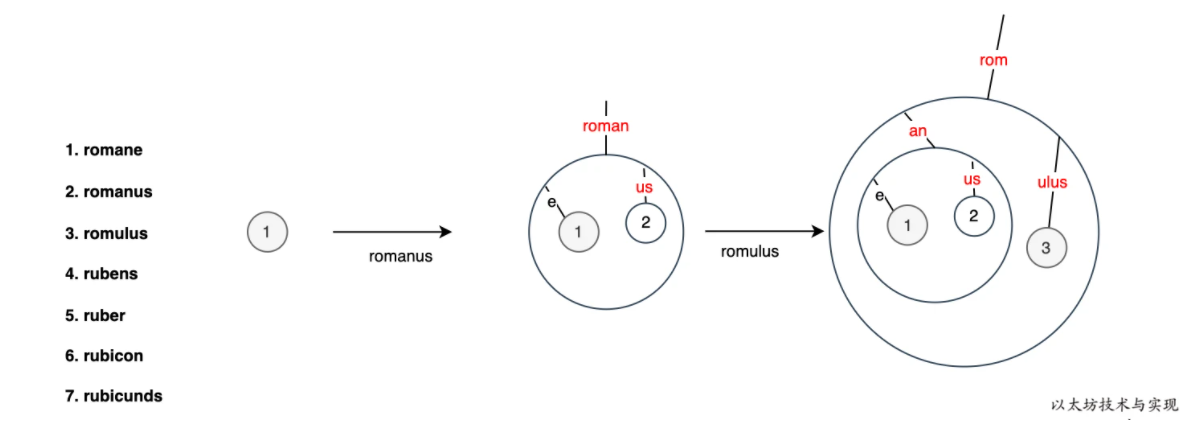
image-20220330162716451

图中的每一个圆圈均代表一个节点，只是节点的类型不同。需要注意的是，图中的红色字部分，实际是一个短节点（shortNode）。 比如，红色的“roman“ 短节点的 key 为 roman, value 是分支节点。继续写入 rubens、ruber、rubicon 的变化过程如下：

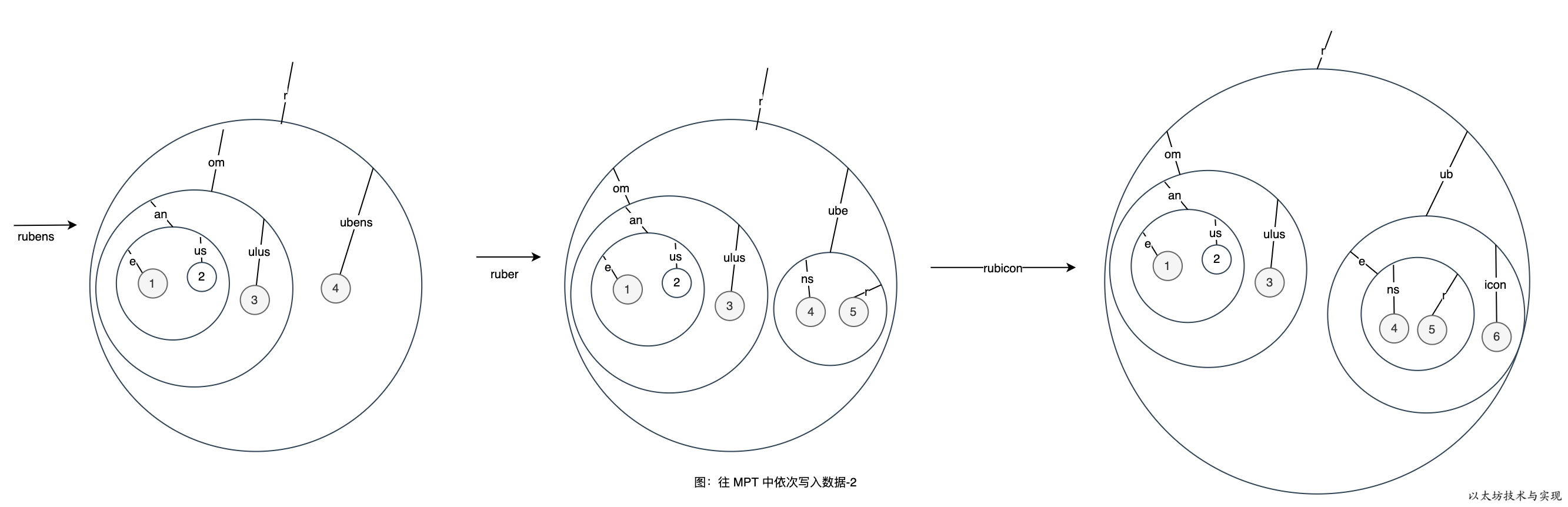
以太坊技术与实现-图-20191127165900.png

将节点写入到 Trie 的内存数据库

如果要把节点写入到内存数据库，需要序列化，可以先去了解下以太坊的 Rlp 编码。这部分工作由trie.Commit()完成，当trie.Commit(nil)，会执行序列化和缓存等操作，序列化之后是使用的Compact Encoding进行编码，从而达到节省空间的目的。

1
2
3
4
5
6
7
8
9
10
11
func (t *Trie) Commit(onleaf LeafCallback) (root common.Hash, err error) {
	if t.db == nil {
		panic("commit called on trie with nil database")
	}
	hash, cached, err := t.hashRoot(t.db, onleaf)
	if err != nil {
		return common.Hash{}, err
	}
	t.root = cached
	return common.BytesToHash(hash.(hashNode)), nil
}

上述代码大概讲了这些：

  • 每次执行Commit()，该 trie 的cachegen就会加 1
  • Commit()方法返回的是trie.root所指向的node的hash（未编码）
  • 其中的hashRoot()方法目的是返回trie.root所指向的node的hash以及每个节点都带有各自hash的trie树的root。
1
2
3
4
5
6
7
8
9
//为每个node生成一个hash
func (t *Trie) hashRoot(db *Database, onleaf LeafCallback) (node, node, error) {
	if t.root == nil {
		return hashNode(emptyRoot.Bytes()), nil, nil
	}
	h := newHasher(onleaf)
	defer returnHasherToPool(h)
	return h.hash(t.root, db, true) //为每个节点生成一个未编码的hash
}

而hashRoot的核心方法就是 h.hash，它返回了头节点的hash以及每个子节点都带有hash的头节点（Trie.root 指向它），大致做了以下几件事：

①：如果我们不存储节点，而只是哈希，则从缓存中获取数据

1
2
3
4
5
6
7
8
9
10
11
12
13
if hash, dirty := n.cache(); hash != nil {
		if db == nil {
			return hash, n, nil
		}
		if !dirty {
			switch n.(type) {
			case *fullNode, *shortNode:
				return hash, hash, nil
			default:
				return hash, n, nil
			}
		}
	}

②：递归调用h.hashChildren，求出所有的子节点的hash值，再把原有的子节点替换成现在子节点的hash值

2.1:如果节点是shortNode

首先把collapsed.Key从Hex Encoding 替换成 Compact Encoding, 然后递归调用hash方法计算子节点的hash和cache，从而把子节点替换成了子节点的hash值

1
2
3
4
5
6
7
8
9
10
11
collapsed, cached := n.copy(), n.copy()
		collapsed.Key = hexToCompact(n.Key)
		cached.Key = common.CopyBytes(n.Key)

		if _, ok := n.Val.(valueNode); !ok {
			collapsed.Val, cached.Val, err = h.hash(n.Val, db, false)
			if err != nil {
				return original, original, err
			}
		}
		return collapsed, cached, nil

2.2:节点是 fullNode

遍历每个子节点，把子节点替换成子节点的Hash值，否则的化这个节点没有children。直接返回。

1
2
3
4
5
6
7
8
9
10
11
12
collapsed, cached := n.copy(), n.copy()

for i := 0; i < 16; i++ {
	if n.Children[i] != nil {
		collapsed.Children[i], cached.Children[i], err = h.hash(n.Children[i], db, false)
		if err != nil {
			return original, original, err
		}
	}
}
cached.Children[16] = n.Children[16]
return collapsed, cached, nil

③：存储节点 n 的哈希值，如果我们指定了存储层，它会写对应的键/值对

store()方法主要就做了两件事：

  • rlp序列化collapsed节点并将其插入 db 磁盘中
  • 生成当前节点的hash
  • 将节点哈希插入db

3.1：空数据或者 hashNode，则不处理

1
2
3
if _, isHash := n.(hashNode); n == nil || isHash {
		return n, nil
	}

3.2:生成节点的 RLP 编码

1
2
3
4
5
6
7
8
9
10
11
12
h.tmp.Reset()                                 // 缓存初始化
	if err := rlp.Encode(&h.tmp, n); err != nil { //将当前node序列化
		panic("encode error: " + err.Error())
	}
	if len(h.tmp) < 32 && !force {
		return n, nil // Nodes smaller than 32 bytes are stored inside their parent 编码后的node长度小于32，若force为true，则可确保所有节点都被编码
	}
//长度过大的，则都将被新计算出来的hash取代
	hash, _ := n.cache() //取出当前节点的hash
	if hash == nil {
		hash = h.makeHashNode(h.tmp) //生成哈希node
	}

3.3:将 Trie 节点合并到中间内存缓存中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
hash := common.BytesToHash(hash)
		db.lock.Lock()
		db.insert(hash, h.tmp, n)
		db.lock.Unlock()
		// Track external references from account->storage trie
		//跟踪帐户->存储Trie中的外部引用
		if h.onleaf != nil {
			switch n := n.(type) {
			case *shortNode:
				if child, ok := n.Val.(valueNode); ok {  //指向的是分支节点
					h.onleaf(child, hash) //用于统计当前节点的信息，比如当前节点有几个子节点，当前有效的节点数
				}
			case *fullNode:
				for i := 0; i < 16; i++ {
					if child, ok := n.Children[i].(valueNode); ok {
						h.onleaf(child, hash)
					}
				}
			}
		}

到此为止将节点写入到Trie的内存数据库就已经完成了。

如果觉得文章不错可以关注公众号：区块链技术栈，详细的所有以太坊源码分析文章内容以及代码资料都在其中。

Trie 树缓存机制

Trie树的结构里面有两个参数， 一个是cachegen,一个是cachelimit。这两个参数就是cache控制的参数。 Trie树每一次调用Commit方法，会导致当前的cachegen增加 1。

1
2
3
4
5
func (t *Trie) Commit(onleaf LeafCallback) (root common.Hash, err error) {
   ...
    t.cachegen++
   ...
}

然后在Trie树插入的时候，会把当前的cachegen存放到节点中。

1
2
3
4
5
6
7
func (t *Trie) insert(n node, prefix, key []byte, value node) (bool, node, error) {
            ....
            return true, &shortNode{n.Key, nn, t.newFlag()}, nil
}
func (t *Trie) newFlag() nodeFlag {
    return nodeFlag{dirty: true, gen: t.cachegen}
}

如果 trie.cachegen - node.cachegen > cachelimit，就可以把节点从内存里面拿掉。 也就是说节点经过几次Commit，都没有修改，那么就把节点从内存里面干掉。 只要trie路径上新增或者删除一个节点，整个路径的节点都需要重新实例化，也就是节点中的nodeFlag被初始化了。都需要重新更新到db磁盘。

拿掉节点过程在 hasher.hash方法中， 这个方法是在commit的时候调用。如果方法的canUnload方法调用返回真，那么就拿掉节点，如果只返回了hash节点，而没有返回node节点，这样节点就没有引用，不久就会被 gc 清除掉。 节点被拿掉之后，会用一个hashNode节点来表示这个节点以及其子节点。 如果后续需要使用，可以通过方法把这个节点加载到内存里面来。

1
2
3
4
5
6
func (h *hasher) hash(n node, db *Database, force bool) (node, node, error) {
   	....
       // 从缓存中卸载节点。它的所有子节点将具有较低或相等的缓存世代号码。
       cacheUnloadCounter.Inc(1)
  ...
}

参考资料：

  1. 详解以太坊默克尔压缩前缀树-MPT :: 以太坊技术与实现 (learnblockchain.cn)
  2. 死磕以太坊源码分析之 MPT 树-上 | mindcarver
  3. 死磕以太坊源码分析之 MPT 树-下 | mindcarver