1. Haskell(一)入门
  2. Haskell(二)函数式编程
  3. Haskell(三) Monad
  4. Haskell(四)总结和工具链
  5. Haskell(五) 总结和展望
  6. Haskell(六) Project Euler 练习1-26

前言

我并不是相关数学理论研究者，而是 Haskell 和 Program language 的爱好者，研究水平还比较低，所以理解有错误是可能发生的，非常欢迎交流和指正。文章中引用了其他博客，我都已经明确注明来源和附带链接，如果您是这些博客的作者，也不同意被引用，那么请联系我。本文借用了 GPT4 写作，提供了非常多的指导。AI 正在改变学习的方式。

另外，我希望读者有一定的近世代数基础，也有一定的编程范式的理解，比如函数式语言（FP），特别是代码讲解都是基于 Haskell。由于我并没有实际的 Haskell 开发经验，所以我不熟悉 Monad的实际应用和用法，这篇文章只是给一个 demo，用于了解编程中的 Monad 的概念。

最后，对于 PL 和 software analysis 爱好者和研究者，可能我不多的感触是，学习一些抽象代数是很有助于锻炼思维的，不只一个老师这样提过建议了。

具体内容可以参考：https://wiki.haskell.org/Monad_tutorials_timeline

理论介绍

Monad 的应用

Monad 是函数式编程中一个重要的抽象概念，它能够帮助我们有效地处理函数组合、副作用等问题。在许多编程语言（如 Haskell、Scala、Rust 等）中，Monad 都有广泛的应用。

下面是一些常见的Monad及其用途：

  1. Maybe Monad（在一些语言中叫 Option Monad）：这种 Monad 常用于处理可能存在的错误或缺失值。它通常包含两种值：Just a（表示有值）和Nothing（表示无值）。这种方式可以避免显示的错误检查，让代码更简洁。
  2. List Monad：这种 Monad 可以用来处理具有多个可能结果的计算。List Monad 将多个可能的结果视为一种副作用，并提供了一种结构化的方式来处理这种副作用。比如说 [1,2] >>= \x -> return (x+1)
  3. IO Monad：这是一个特殊的 Monad，用于处理那些可能带有副作用的 I/O 操作。在纯函数式编程语言中，I/O 操作会破坏函数的纯粹性，因此通过 IO Monad，我们可以在不破坏纯函数性质的情况下，进行 I/O 操作。
  4. State Monad：这种 Monad 可以用来在纯函数式编程中模拟带有状态的计算。通过 State Monad，我们可以在不直接修改变量的情况下，进行状态的更新。
  5. DBIO Monad：这是一种用于数据库交互的 Monad。DBIO 代表数据库 I/O，它允许你以一种声明式、纯函数式的方式编写数据库操作，同时确保操作的原子性和一致性。

以上只是一些最常见的 Monad 的应用，实际上 Monad 的应用非常广泛。任何可以用Monad laws（即Monad的三个基本法则：左单位律、右单位律和结合律）描述的结构，都可以看作是一个 Monad，都可以利用 Monad 提供的优雅、强大的函数式编程工具进行处理。

Monad 的必要性

下面引用的内容来自「什么是 Monad (Functional Programming)？ - 刘月半的回答 - 知乎 」。因为他说明了 Monad 在错误处理方面的优势，简单地说，就是可以通过定义规则，统一地处理，而不是那么复杂每一步都错误处理。

一个自函子范畴上的幺半群

程序语言中有一种常见的构造「函子」（functor）。Haskell 里的 Maybe 是个很好的例子：
(作者补充：a 可以是一个类型，然后 Maybe 的 Kind 就从 *->* 变成了 *，可以类比泛型 >)

1
data Maybe a = Just a | Nothing

(作者补充 *->* 通过推导变成了 *，但是我们有时候要用第一个，有时候要用第二个，那么 fmap 就是用来提取第二个，提取出来给 f 操作之后又放回 *->*，变成*)
Maybe 之所以是函子，是因为它可以通过 fmap（functor map）把所有的函数拎到「Maybe 空间」里。换而言之，令 f :: a -> b，fmap f :: Maybe a -> Maybe b。fmap 定义如下：

1
2
3
4
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap f mbx = case mbx of
  Just x  -> Just (f x)
  Nothing -> Nothing

Maybe 可以方便地用来做错误处理。对于那些不支持 Maybe 作输入的函数，我们也可以通过 fmap 兼容之。但是，组合多个会产生 Maybe 的函数很麻烦。比如说这个除法函数：

1
2
3
safeDiv :: Int -> Int -> Maybe Int
  safeDiv _ 0 = Nothing
  safeDiv x y = Just (x / y)

考虑一下表达式：

1
2
3
4
5
6
7
case safeDiv a b of
  Nothing -> Nothing
  Just x  -> case safeDiv c x of
    Nothing -> Nothing
    Just y  -> case safeDiv d y of
      Nothing -> Nothing
      Just z  -> safeDiv e z

在 JavaScript 界，我们管这样的代码叫「callback hell」。不过这段代码总比下面这段好：

1
2
3
4
let x = safeDiv a b
    y = fmap (safeDiv c) x
    z = (fmap . fmap) (safeDiv d) y
    in (fmap . fmap . fmap) (safeDiv e) z

他提到的回调地狱，实际上是说 Monad 可以任意层等封装和解封装。「怎样用简单的语言解释 Monad？ - Belleve 的回答 - 知乎」这里有部分图片，就解释的比较清楚。

使用 join 诠释的话，Monad 会有一个非常不同的理解：Monad 是可以增（return/unit）减（join）层数的「箱子」。而 unit 和 join 因为满足某些定律所以形成了一个幺半群（对，这就是那老梗）。所以，Monad 代表的是层次，而不是顺序。（回想下 CPS，是不是用层次表示顺序的？）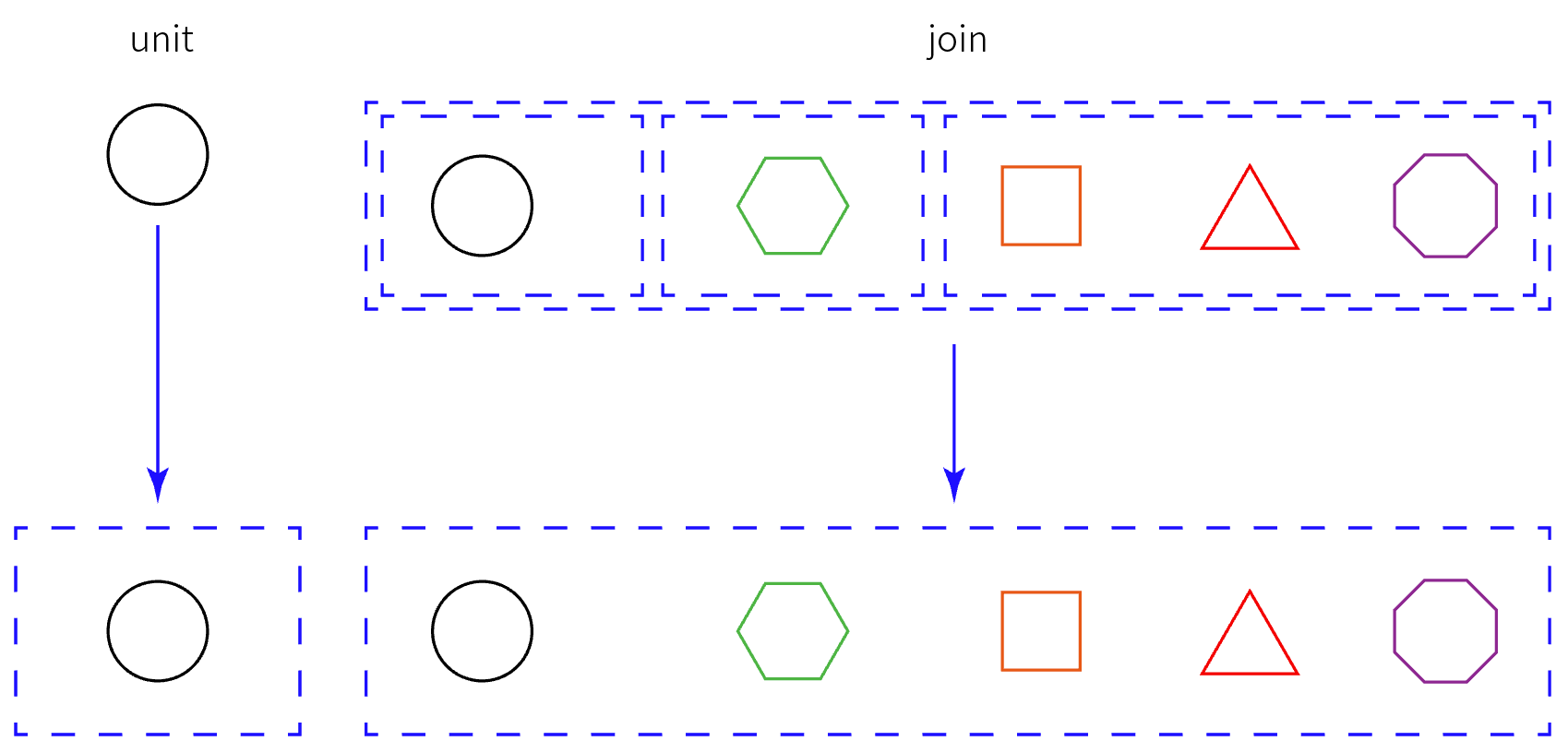

img

Haskell 的 bind 可以看作 fmap 和 join 的复合

img

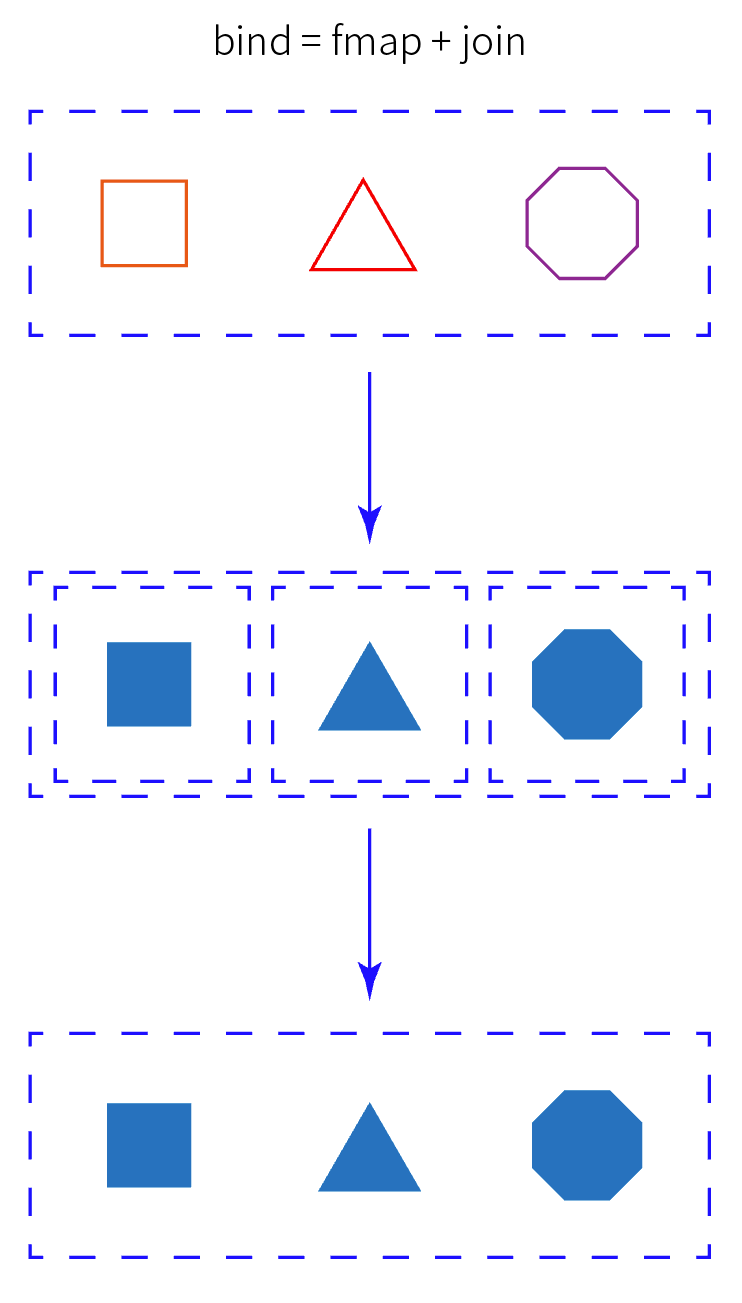
首先解释 Endofunctor，Endofunctor 是（不加限制的）箱子，它把类型（一个类型范畴里的对象）T 装进去变成 F(T)，同时还能保证所有函数（态射）A->B，都有一个带箱子的版本 F(A)->F(B)。

而 Monad 呢？就是除了前面的两个箱子，我们还能定义出把任意类型的数值装进箱子的 unit：T->F(T)，以及把两层箱子只留一层的 join：F(F(T))->F(T)。

Monad laws

下面内容看不太懂，太正常不过了，读者只需要有一个印象。等阅读了后面的代码详解，理解思路和用法，从使用的规律去看待它的性质，会有不一样的体会。

Monad laws 是指三个性质，这些性质定义了一个有效的 Monad 应该如何表现。这些法则在所有的 Monad 实例中都应该成立，以确保在 Monad 的计算中可以进行一些有用的推理和转换。具体来说，这三个法则是：

  1. 左恒等法则 (Left Identity)：如果我们将一个值用 return 放入一个 Monad，然后应用函数 f，那么结果应该和直接将该值应用到 f 是一样的。用公式表示就是 return a >>= f == f a
    比如说，(return 1) 返回了 (Monad m, Num a) => m a 类型的 monad，然后呢 f 是 (\x -> return (x*2))，类型为 (Monad m, Num a) => a -> m a。那么得到的结果 (return 5) >>=(\x -> return (x\*2)) 应该等于 (\x -> return (x*2)) 5

  2. 右恒等法则 (Right Identity)：如果我们有一个 Monad 值 m，然后我们用 return 作为 bind 操作的右操作数，那么结果就应该等于原来的 Monad 值。用公式表示就是 m >>= return == m。比如 m 是 return 4 类型为 (Monad m, Num a) => m a，那么 ((return 4) >>= return) 的类型是 (Monad m, Num b) => m b。

  3. 结合律 (Associativity)：当我们有三个操作串在一起时，应用的顺序不应该影响结果。也就是说，我们应该可以在不改变结果的情况下，改变括号的位置。用公式表示就是 (m >>= f) >>= g == m >>= (\x -> f x >>= g)。
    比如定义 f x= return (2*x), g x= return (x+1)，m= return 4，注意 return 的优先级很高，需要括号。那么左边应该是 9，类型为 (Monad m, Num b) => m b， 右边的结果也是完全一样的。注意 m >>= (f>>= g) 语法是错的，因为 g 需要 monad 类型，而不是 (Monad m, Num a) => a -> m a

Monad laws 为我们提供了一种方法来推理我们的 Monad 代码，并确保它的行为是一致的。如果你创建自己的 Monad 实例，那么你应该确保这些法则在你的实例中成立。

代码示例

基础介绍

注意，这是基于 ghc-9.2.7 的 Haskell 版本，语法可能是 9.0 之后的了。另外，前置知识实在太多，比如说介绍 Monad laws 时的类型签名，可能读者理解起来都有些困难。读者可以阅读我的 Haskell 文章：

使用 Monad 可以使错误处理更加简洁和高效。这是因为 Monad 提供了一种方式，允许你将可能产生错误的计算组合在一起，
同时在计算的过程中，一旦检测到错误，计算就会立即停止，并返回一个表示错误的值。

我们可以将多个可能产生错误的函数使用 >>= 运算符链接起来。当每一个函数在其运算过程中产生一个错误（即返回 Nothing）时，
整个链条上的后续计算就会立即停止，而不需要进一步的错误检查。

再者，Monad 也可以帮助你处理其他种类的副作用，比如输入/输出、状态变化、异常处理等等。这是因为 Monad 提供了一种将复杂操作封装成单个值的方式，这样你就可以像处理普通的值一样来处理这些操作。
在这个过程中，Monad 为你处理了所有复杂的细节。

Monad一般有如下几个部分组成，任何 Monad 都是一个 Applicative，任何 Applicative 都是一个 Functor。

标注:L 对于一个 Monad，表示为 m a,其中 a 叫做 monad 的封装的值，m 叫做 monad 构造器。

  • Functor：提供了一个基本的映射操作 fmap。fmap 接收一个函数和一个 Functor ，然后将这个函数作用于 Functor 中封装的值。
  • Applicative：扩展了 Functor，增加了更多操作。它的核心是一个叫做 <*> 的操作符，它允许我们通过 liftA2 等函数或者直接使用<*>，对封装好的变量（也就是 m a）操作。此外，Applicative 还提供了 pure 函数，用于将一个普通的值放入 Applicative 上下文中。
  • Monad：再次扩展了 Applicative，提供了一个新的操作>>=(也叫 bind 操作)。它接收一个 Monad 值和一个函数，这个函数接收一个普通的值，返回一个 Monad 值。通过 bind 操作，我们可以更方便地将多个 Monad 操作链接在一起。

作者并不熟悉这些定义在数学上的差别

Functor

Functor 是能够通过 fmap 函数将一个普通函数映射到某种结构中的类型。这使得你可以将函数作用于这种结构中的值，而不需要关心结构的具体内容。可以 f 类比上面的 m。

1
2
class Functor f where
    fmap :: (a -> b) -> f a -> f b

fmap 可以把 functor 封装的值类型的函数，映射到 functor 的函数。比如说下面 f 只能处理 数值，比如 f 2 =4，g 封装之后 可以处理 f (return 2)，返回 Monad f => f Int 的 4

1
2
3
4
5
f :: Int -> Int
f x = 2 * x

g:: (Functor f) => f Int -> f Int
g = fmap f

Applicative

Applicative Functor (通常简称为 Applicative) 是 Functor 的一种扩展，提供了在 Functor 的基础上进行更复杂操作的能力。Applicative 提供了 pure 函数，用于将普通值放入 Applicative 结构，以及 <*> 操作符，使得你可以在不需要拆解 Applicative 结构的情况下进行更复杂的计算。

下面就通过 pure 代替 return，封装了函数 f，而 <*>::Applicative f => f (a -> b) -> f a -> f b，所以

1
2
3
4
5
f :: Int -> Int
f x = 2 * x

h :: (Applicative f) => f (Int -> Int)
h = pure f

Monad

Monad 是 Applicative 的一种扩展，提供了更强大的组合操作的能力。特别的，Monad 提供了>>=操作符 (也叫 bind 操作)，这个操作可以将一个产生 Monad 值的函数应用于另一个 Monad 值。这使得你可以根据一个 Monad 值的结果来决定进行下一步的计算，这是 Functor 和 Applicative 无法做到的。
下面是为自定义的 Wrapper 类型，实现了三种特殊的类型类。Wrapper 可以为 Num 类型类的类型，实现自己定义的 +, -, *, 除,返回符号的功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
module Main where

-- 隐藏默认的typeclasee，然后自己重新定义
import Prelude hiding (Applicative, Functor, Monad, fmap, pure, return, (>>=))

class (Functor f) => Applicative f where
  pure :: a -> f a
  (<*>) :: f (a -> b) -> f a -> f b

class Functor f where
  fmap :: (a -> b) -> f a -> f b

class (Applicative m) => Monad m where
  (>>=) :: forall a b. m a -> (a -> m b) -> m b
  return :: a -> m a
--------------------------------------------
-- 自定义类型
data Wrapper a = Ok a | Err String

ok :: a -> Wrapper a
ok = Ok
--------------------------------------------
-- 实现这些typeclass
instance Functor Wrapper where
  fmap f (Ok x) = Ok (f x)
  fmap _ (Err msg) = Err msg

instance Applicative Wrapper where
  pure = Ok
  (Ok f) <*> (Ok x) = Ok (f x)
  (Err msg) <*> _ = Err msg
  _ <*> (Err msg) = Err msg

instance Monad Wrapper where
  (Ok x) >>= f = f x
  (Err msg) >>= _ = Err msg
  return = Ok
--------------------------------------------
-- 实现自定义的操作
instance (Num a) => Num (Wrapper a) where
  (Ok x) + (Ok y) = Ok (x + y)
  (Err msg) + _ = Err msg
  _ + (Err msg) = Err msg

  (Ok x) - (Ok y) = Ok (x - y)
  (Err msg) - _ = Err msg
  _ - (Err msg) = Err msg

  (Ok x) * (Ok y) = Ok (x * y)
  (Err msg) * _ = Err msg
  _ * (Err msg) = Err msg

  abs (Ok x) = Ok (abs x)
  abs (Err msg) = Err msg

  signum (Ok x) = Ok (signum x)
  signum (Err msg) = Err msg

  fromInteger x = Ok (fromInteger x)

instance (Fractional a, Eq a) => Fractional (Wrapper a) where
  (Ok x) / (Ok 0) = Err "Division by zero"
  (Ok x) / (Ok y) = Ok (x / y)
  (Err msg) / _ = Err msg
  _ / (Err msg) = Err msg

  fromRational r = Ok (fromRational r)

instance (Show a) => Show (Wrapper a) where
  show (Ok x) = "Ok " ++ show x
  show (Err msg) = "Err " ++ msg
--------------------------------------------
-- 用于显示特性的例子
divideAndAdd :: (Eq a, Fractional a) => Wrapper a -> Wrapper a -> Wrapper a -> Wrapper a -> Wrapper a
divideAndAdd x1 y1 x2 y2 = x1 / y1 >>= \result1 -> x2 / y2 >>= \result2 -> return (result1 + result2)

divideAndAdd2 :: (Eq a, Fractional a) => Wrapper a -> Wrapper a -> Wrapper a -> Wrapper a -> Wrapper a
divideAndAdd2 x1 y1 x2 y2 = x1 / y1 + x2 / y2
--------------------------------------------
main = print $ divideAndAdd 1 0 1 0


总结

Functor（函子）：允许你通过 fmap 或 <$> 将普通函数应用到上下文中的值。

Applicative（应用函子）：扩展了 Functor 的概念，通过 <*> 运算符允许在上下文中组合函数。它使得可以处理多个包含上下文的值。

Monad（单子）：通过 >>=（绑定运算符）提供了一种链式组合计算的方法，允许在处理前一个计算的结果时定义下一个计算。这对于处理有序的、依赖于之前计算结果的操作至关重要。