信息论与编码

1. C语言基础
2. 乘法逆元
3. 信息安全算法基础
4. 操作系统基础
5. x86汇编基础
6. 信息论与编码

前言

这篇总结和系统性学习地笔记，是基于电子科技大学的《信息论与编码》课程，而我写作的初衷是个人的复习。因此，内容可能不是那么详细，但是我会保证基本上我会在自己理解的基础上，完成这篇文章。随着我自己的理解的加深，可能会出现前后不一致的情况，如果读者感到矛盾，那么请在评论区说明，等我有时间时会继续完善的。

离散信源熵

单符号离散信源是最简单的情况，离散是指信源输出是有限个符号，单符号是指每个符号都是独立的，每次只发出一个符号。

随机变量基础

在单符号离散信源中，每个符号的概率分布可以用一个概率向量来表示。例如，一个三个符号的单符号离散信源可以用以下概率分布表示，符号 A、B、C 之间是相互独立的，即一个符号的出现不会影响到其他符号的出现概率。可以如下的方式抽象成数学模型。

离散随机变量集合：${a_1,a_2,a_3}$，对应概率 $P(a_i)$，且 $0 \le P(a_i) \le 1$ , $\sum{p\left( a_i \right)}=1$.

符号	出现概率
A	0.2
B	0.3
C	0.5

对于二维随机变量，也是有类似的结论，比较特殊一点的是，

$$\begin{aligned} & \sum_{j=1}^m{p}\left( b_j/a_i \right) =1\\ &\sum_{j=1}^m{\sum_{i=1}^n{p}}\left( a_ib_j \right) =1 \\ &\sum_{i=1}^n{p}\left( a_ib_j \right) =p\left( b_j \right) \\ &p\left( a_ib_j \right) =p\left( b_j \right) p\left( a_i/b_j \right) =p\left( a_i \right) p\left( b_j/a_i \right) \end{aligned}$$

对于随机变量独立的情况，可以同时发生可以拆开成乘法，条件概率没有影响。

$$p\left( a_ib_j \right) =p\left( a_i \right) p\left( b_j \right) ,p\left( b_j/a_i \right) =p\left( b_j \right) ,p\left( a_i/b_j \right) =p\left( a_i \right)$$

信息量

在有了概率分布的基础之后，就可以开始学习基于统计的自信息量的概念了。一定记住公式，单位是 bit

$$I\left( a_i \right) =-\log _2p\left( a_i \right)$$

需要注意的性质，自信息量的范围是 $(0,+\infty)$，而且是单减函数。

对于联合变量，有联合自信息量，计算公式也是类似的：

$$I\left( a_ib_i \right) =-\log _2p\left( a_ib_i \right)$$

特别的，当互相独立时，就可以拆开：

$$I(a_ib_i)=I(a_i)+I(b_i)$$

条件信息量则除了计算公式，还和自信息量、联合信息量有直接关系。简单说，就是 a 的信息量+a 已经发生后 b 发生的信息量，就是 a 和 b 同时发生的信息量：

$$\begin{aligned} I\left( a_ib_j \right) &=-\log p\left( a_ib_j \right)\\ &=-\log p\left( a_i \right) p\left( b_j/a_i \right) =I\left( a_i \right) +I\left( b_j/a_i \right)\\ &=-\log p\left( b_j \right) p\left( a_i/b_j \right) =I\left( b_j \right) +I\left( a_i/b_j \right)\\ \end{aligned}$$

以上，讨论了单个符号的信息量和联合信息量的定义，一个单符号离散信源会有多个符号，就提出了衡量信源信息量的信源熵，简单地说，就是每个符号的信息量的平均值，或者信源的平均不确定度、随机性，单位是 bit/sign：

$$H(X)=E\left[ I\left( a_i \right) \right] =E\left[ -\log _2p\left( a_i \right) \right] =-\sum_{i=1}^n{p}\left( a_i \right) \log _2p\left( a_i \right)$$

信源熵

如果同时考虑两个信源，要计算条件熵，可以根据数学期望的定义，得到：

$$H(X/Y)=E\left[ I\left( a_i/b_j \right) \right] =\sum_{j=1}^m{\sum_{i=1}^n{p}}\left( a_ib_j \right) I\left( a_i/b_j \right)$$

这里必须注意，出现 $I(a_i/b_j)$ 的概率是 $a_i$ 和 $b_j$ 同时发生。也可以用如下的办法推理，一次只考虑一个随机变量：

$$\begin{align*} &\because H\left( X/b_j \right) =\sum_{i=1}^n{p}\left( a_i/b_j \right) I\left( a_i/b_j \right) =-\sum_{i=1}^n{p}\left( a_i/b_j \right) \log p\left( a_i/b_j \right) \\ &H(X/Y)=\sum_{j=1}^m{p}\left( b_j \right) H\left( X/b_j \right) \\ &=-\sum_{j=1}^m{\sum_{i=1}^n{p\left( b_j \right) p\left( a_i/b_j \right) \log p\left( a_i/b_j \right)}}\\ &=-\sum_{j=1}^m{\sum_{i=1}^n{p\left( a_ib_j \right) \log p\left( a_i/b_j \right)}}\\ \end{align*}$$

显然的，因为 $p(a_ib_i)<p(a_i)$ 且 $p(a_i)$

对于联合熵，也是一样的做法。而且类似于联合信息量，和单独的信源熵和条件信源熵有关

$$\begin{align*} &H(XY)=\sum_{i=1}^n{\sum_{j=1}^m{p}}\left( a_ib_j \right) I\left( a_ib_j \right) =-\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_i \right) p\left( b_j|a_i \right) \log _2p\left( a_i \right) p\left( b_j|a_i \right)}} \\ &=-\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_i \right) p\left( b_j|a_i \right) \log _2p\left( a_i \right)}}-\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_i \right) p\left( b_j|a_i \right) \log _2p\left( b_j|a_i \right)}} \\ &=-\sum_{i=1}^n{p\left( a_i \right) \log _2p\left( a_i \right)-}\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_ib_i \right) \log _2p\left( b_j|a_i \right)}} \\ &=H\left( X \right) +H\left( Y/X \right) \\ &=H\left( Y \right) +H\left( X/Y \right) \end{align*}$$

而且可以由于信源熵是非负数，可以发现联合信源不确定性更大。

$$\begin{gather*} &H(XY)\ge H(X),\ H(XY)\ge H(Y)\\ &H(XY)\ge H(Y/X),\ H(XY)\ge H(X/Y) \end{gather*}$$

信源熵很重要的性质就是，当信源 X 的 n 个符号，每个符号概率相等时，信源熵取得最大值 $H(X)=\log _2n$，因为

$$\begin{align*} &\because \ln x\le x-1, x>0 \ and\,\,\log _2x=\frac{\ln x}{\ln 2}\\ &H\left( X \right) =\sum_{i=1}^n{p\left( a_i \right) \log _2\frac{n}{np\left( a_i \right)}=}\sum_{i=1}^n{p\left( a_i \right) \log _2n}+\sum_{i=1}^n{p\left( a_i \right) \log _2\frac{1}{np\left( a_i \right)}} \\ &=\log _2n+\sum_{i=1}^n{p\left( a_i \right) \log _2\frac{1}{np\left( a_i \right)}=}\log _2n+\frac{1}{\ln 2}\sum_{i=1}^n{p\left( a_i \right) \ln \frac{1}{np\left( a_i \right)}} \\ &\le \log _2n+\frac{1}{\ln 2}\sum_{i=1}^n{p\left( a_i \right) \left( \frac{1}{np\left( a_i \right)}-1 \right)} \\ &=\log _2n+\frac{1}{\ln 2}\left( 1-\sum_{i=1}^n{p\left( a_i \right)} \right) =\log _2n \end{align*}$$

另外值得注意的是，因为 $\lim _{\varepsilon \rightarrow 0} \varepsilon \log \varepsilon=0$ 所以小概率事件实际上对信源熵的贡献比较小。而且信源熵是严格上凸函数。

从信息量的角度，还可以发现 $$H(X)\ge H(X/Y)$$，这叫做极值性。如果 Y 可能包含了 X 的某些信息，那么信源熵就会减少，除非 Y 是确定的，或者是二者不可能同时存在。这不要求证明。

信道编码

信源发出的消息序列通常不能直接送 给信道传输，需要经过信源编码和信道编 码。信道编码的目的是，提高编码的效率，降低差错，压缩信源的冗余度。简单地说， 编码是一种映射，是将输入符号映射成码字。

根据编码的方式，可以分成无失真编码和限失真编码。很显然的，无失真编码的映射需要一一对应，可逆。因此无失真编码只能用在离散信源，不能用在连续信源。比如说模拟信号转化成数字信号，是无法产生无数种字符(数字)，来表示连续的值。

假设这样一个编码过程，离散信源 X 一次产生 L 个字符，也就是每次输出是 ${a_1a_2\dots a_l}$ 这样的序列，这称作 L 元。那么现在要找到一种编码方式，将原来的符号映射成另外一套符号。定长编码定理就是研究这样的编码过程，它提出了，假如编码系统使用的字符有 m 个取值(一般是 2 个，0 和 1)，每次输出 k 个符号 $b_1,b_2,\dots,b_k$，也就是定长地用 K 个字符表示一个符号 ${a_1a_2\dots a_l}$，也即

$$\begin{gather*} & a_1a_2\dots a_l\rightarrow b_{j_1}b_{j_2}\dots b_{j_k}\\ & \mathrm{where} \ j_1,\dots ,j_k\,\,\mathrm{refer}\ \mathrm{to}\ \mathrm{serial}\ \mathrm{numbers} \end{gather*}$$

那么，根据定长编码定理，**如果要尽可能压缩信息，减少编码的长度 K，但是同时要保证无失真编码，那么一定需要满足：编码后 X 的每个符号对应的编码携带的最大信息量，大于 X 的信源熵。**下面的 $\ln m$ 就是编码后的最大信源熵，R 称作信息率。

$$R=\frac{K}{L}\log m\ge H(X)+\varepsilon ,\varepsilon >0,\sigma >0$$

其中，又定义的编码效率：

$$\eta =\frac{H\left( X \right)}{R}$$

变长编码定理则告诉，如果编码的平均长度满足下面的条件，那么一定存在无失真编码，而且信息率 R 大于信源熵：

$$1+\frac{L\times H(X)}{\log m}\ge \overline{K}\ge \frac{L\times H(X)}{\log m}$$

在变长编码定理的框架内，还需要一种系统的编码的方式，确保在变长的码字不会产生歧义，而且接收序列时可以立即匹配编码，不用观察后面的码字。

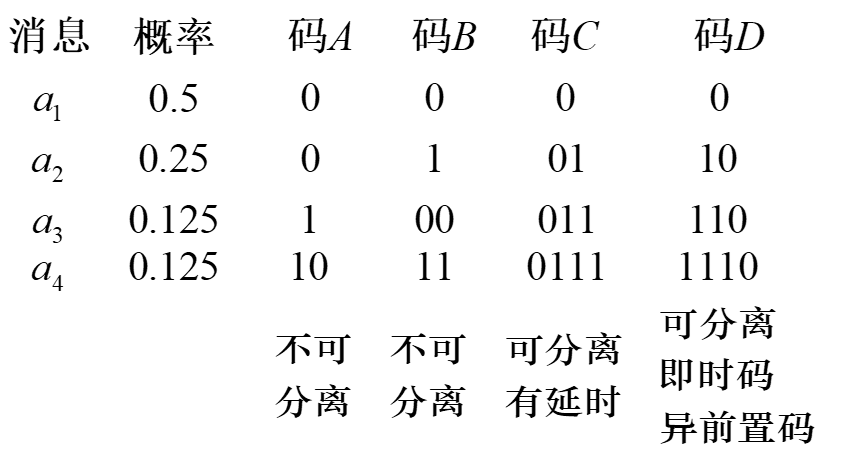
根据克拉夫特不等式，能够找到这样的异前置码编码方式的充要条件是，对于 m 个字符的编码系统，信源 X 的每个字符映射后的字符长度 $k_i$，满足：

$$\sum_{i=1}^n{m^{-k_i}}\le 1$$

香农编码

香农编码就是这样变长编码的一种方式。按信源符号的概率从大到小的顺序排队，然后对每个字符定义累加概率（排在它前面的字符的概率之和），这样就可以得到结论：

$$\begin{gather*} &p_a(0)=0\\ &p_a\left(a_j\right)=\sum_{i=1}^{j-1} p\left(a_i\right), j=1,2, \cdots, n\\ &-\log _2 p\left(a_i\right) \leq k_i \leq 1-\log _2 p\left(a_i\right) \end{gather*}$$

编码则是 $p_a\left(a_j\right)$ 二进制表示的小数点后 $k_i$ 位。参考下面的例题。

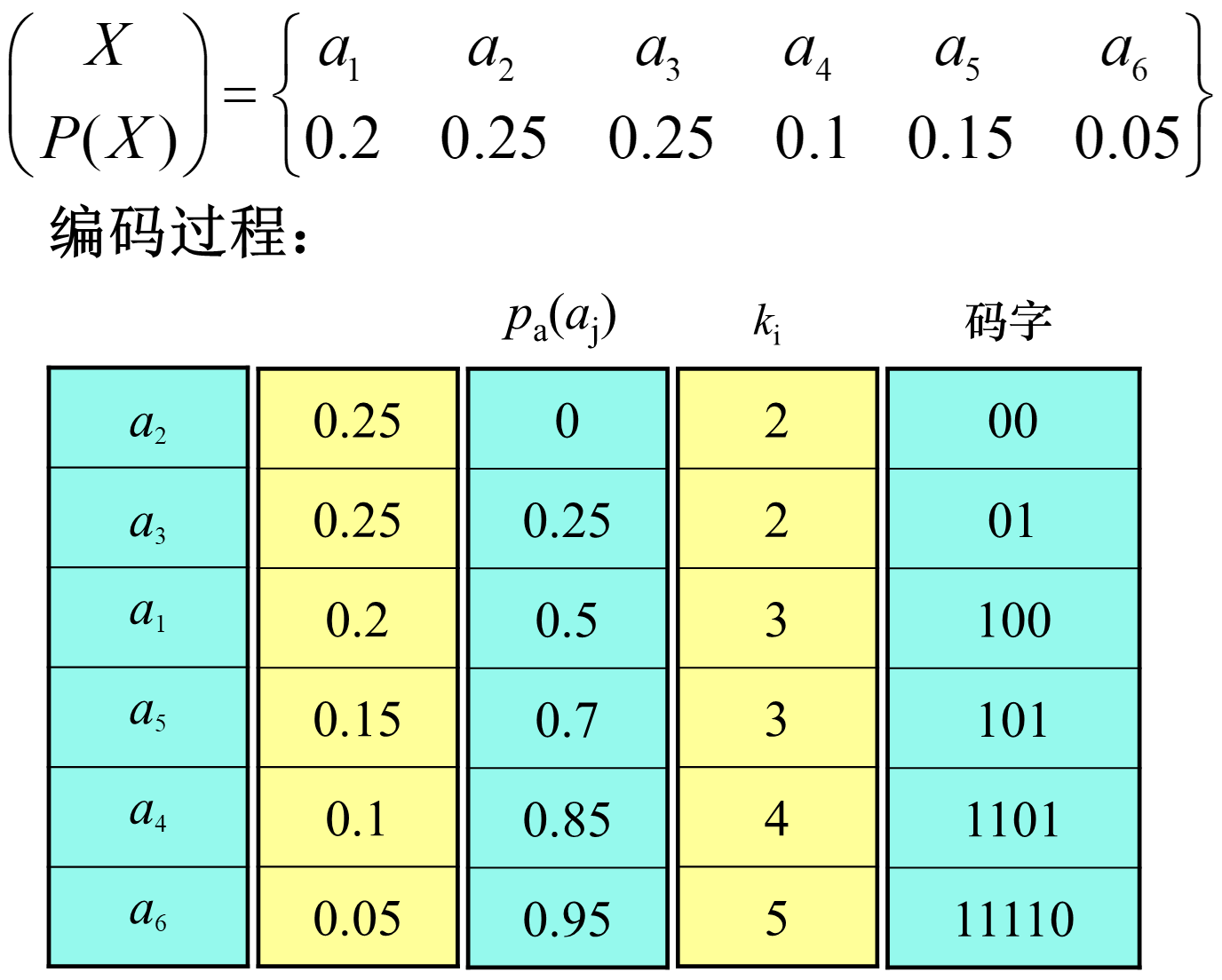
可以计算得到相关参数：

$$\begin{align*} &L=1,\ m=2 \\ &H(X)=2.4233( \mathrm{bit} / \mathrm{sign} ) \\ &\overline{K}=\sum_{i=1}^6{p}\left( a_i \right) k_i=2.7 \\ &R=\frac{\overline{K}}{L}\log _2m=2.7 \\ &\eta =\frac{H(\mathrm{X)}}{R}=89.63\% \end{align*}$$

费诺编码

首先从大到小排队，然后把符号分成 2 组，要求这是所有分成 2 组的情况中，每组概率之和相差最小的情况。然后随意给两组其中一个分配 0，另一个分配 1。每组内部继续按照上面的规则分组和编码。

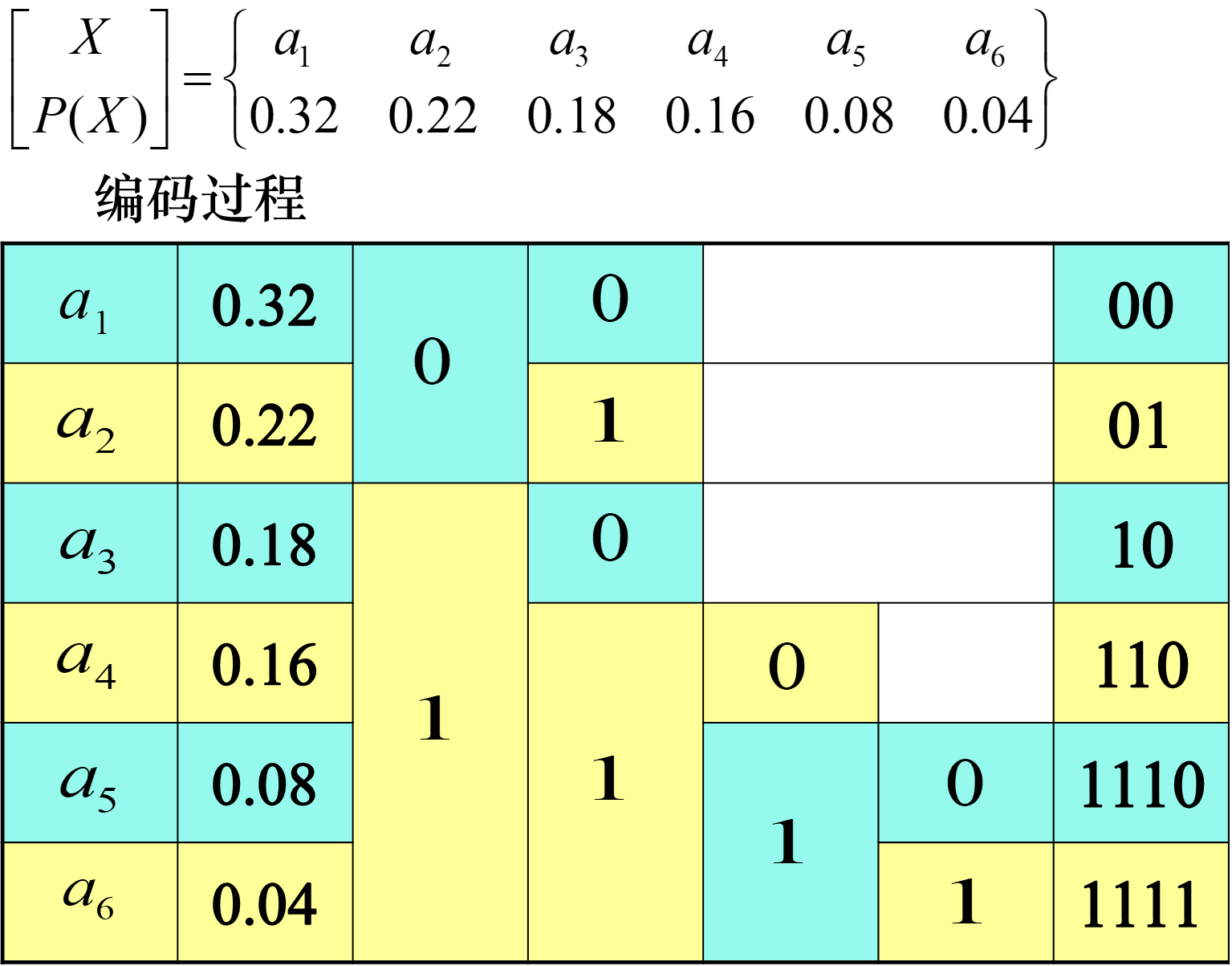
赫夫曼编码

首先从大到小排队，对于符号的概率的 n 种取值，开始构造二叉树，节点是最小的 2 个符号，父节点是他们的和。然后用父节点替代它们，变成 n-1 个符号，去除了之前两个概率最小的符号的概率，增加了一个父节点的概率。重复这个过程，直到只剩下 1 个符号。

下面的序号是代表合并的步骤。

信道容量

信道模型

信道容量（channel capacity）则是指一个信道在特定条件下（例如，特定的信噪比）能够传输的最大信息速率，反映了在单位时间内能够通过信道传输的最大信息量。这里我们不考虑两个信源之间的具体转换关系，而是考虑**两个随机变量之间的信息共享量，或者说，一个随机变量中包含的关于另一个随机变量的信息量。这就是互信息量。**它也可以衡量特征和目标变量之间的相关性。

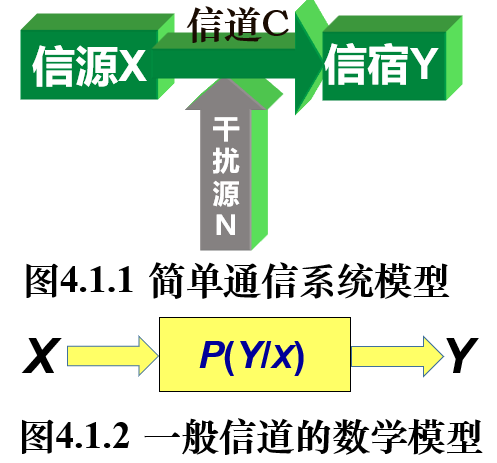
直观地讲，如果 X 和 Y 是独立的，那么他们的互信息就是 0，因为知道 X 的值并不能给我们提供关于 Y 的任何信息，反之亦然。另一方面，如果 X 和 Y 完全相关（也就是说，如果我们知道了 X 的值，那么我们就可以确定 Y 的值），那么他们的互信息量就等于 X（或 Y）的熵。

总之，X 和 Y 之间的互信息量或者说相关性，来自信息的传递，如果没有信息从信道传递，那么就是相互独立的。

互信息量

两个随机变量的某个取值，来自 Y 的取值 b 对来自 X 的取值 a 的互信息量，也就是在已知事件 b 发生后，对事件 a 的不确定性减少的程度，

定义如下：

$$I\left( a;b \right) =\log \frac{p\left( a|b \right)}{p\left( a \right)}$$

这个定义体现了通过信宿 Y 的值 b 来推测信源 X 的值 a，与实际信源 X 的值 a 的概率的比值，也是这一次传输的信息量。如果事件 b 发生了，那么我们对事件 a 的预测可能会更准确一些，也就是说，事件 a 的不确定性可能会降低。而造成这种不确定性的减少的原因，就是信源 X 通过信道传递信息到了信宿 Y。

从自信息量的角度，也可以验证刚才对互信息量的解释。因为在信息传递之前，信源 X 和信宿 Y 是独立的，只有信息传输之后，才会有共享的信息。传递的部分就是信源 X 的信息量，减去从信宿 Y 获取观察信源 X 的信息量：

$$I\left(a_i ; b_j\right)=-\log p\left(a_i\right)+\log p\left(a_i / b_j\right)=I\left(a_i\right)-I\left(a_i / b_j\right)$$

如果从信息共享（也就是信息传递）的角度看，更加直观的形式如下：

$$I\left( a;b \right) =I\left( b;a \right) =\log \frac{p\left( ab \right)}{p\left( a \right) p\left( b \right)}$$

通过简单变形，就有了最开始互信息量的定义，它给我们提供了一种，不知道 $p(b)$ 但是知道 $p(a|b)$ 的情况下的计算方法。

对于两个信源而言，平均互信息量就是所有组合的互信息量的平均值：

$$I\left( X;Y \right) =\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_ib_j \right) \log \frac{p\left( a_ib_j \right)}{p\left( a_i \right) p\left( b_j \right)}}}=\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_ib_j \right) \log \frac{p\left( a_i|b_j \right)}{p\left( a_i \right)}}}$$

注意：

1. 互信息量是可以为正，也可以为负。

2. 但是平均互信息量是非负数。相互独立的时候有 $p(ab)=p(a)p(b)$

   $$\begin{align*} &I\left( X;Y \right) =\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_ib_j \right) \log \frac{p\left( a_ib_j \right)}{p\left( a_i \right) p\left( b_j \right)}}}=\frac{1}{\ln 2}\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_ib_j \right) \ln \frac{p\left( a_ib_j \right)}{p\left( a_i \right) p\left( b_j \right)}}} \\ &=-\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_ib_j \right) \ln \frac{p\left( a_i \right) p\left( b_j \right)}{p\left( a_ib_j \right)}}} \\ &\ge -\sum_{i=1}^n{\sum_{j=1}^m{p\left( a_ib_j \right) \left( \frac{p\left( a_i \right) p\left( b_j \right)}{p\left( a_ib_j \right)}-1 \right)}}=-\sum_{i=1}^n{\sum_{j=1}^m{\left( p\left( a_i \right) p\left( b_j \right) -p\left( a_ib_j \right) \right)}} \\ &=-\left( \sum_{i=1}^n{p\left( a_i \right)}-\sum_{i=1}^n{p\left( a_i \right)} \right) =0 \end{align*}$$

3. 当 X Y 独立的时候，共享的信息为 0，平均互信息量为 0.

4. 共享的信息，无论从 X 的角度还是从 Y 的角度，都是相等的

   $$I\left( Y;X \right) =I\left( X;Y \right)$$

5. 共享的信息量不可能超过信源本身，也就是极值性。当 X 和 Y 一一对应就是无损的信道：

   $$I\left( X;Y \right) \le H\left( X \right) \\ I\left( X;Y \right) \le H\left( Y \right)$$

6. 平均互信息量是 $p(a)$ 的上凸用函数，$p(b|a)$ 的下凸函数。

7. 信息传递递减。假设 X Z 互相独立，经过 Y 传递信息，那么

   $$\begin{aligned} &I(X;Z)\le I(Y;Z)\\ &I(X;Z)\le I(X;Y)\\ &I\left( X;YZ \right) =H\left( X \right) -H\left( X|YZ \right) \end{aligned}$$

条件互信息量

特别地，教材里还提到了条件互信息量，信源 X 和信宿 Y 都知道一个条件 c，那么定义在条件 c 下的 a b 的互信息量为：

$$I\left( a;b|c \right) =I\left( \left( a;b \right) |c \right) =\log \frac{p\left( a|bc \right)}{p\left( a|c \right)}$$

这里要稍微注意的是，条件互信息量的表示，容易有歧义。c 是共有的条件。特别的，如果把 b c 所在的信源作为一个整体，a 所在信源作为信宿，有：

$$I\left( a;bc \right) =I\left( a;c \right) +I\left( a;b|c \right) =I\left( a;b \right) +I\left( a;c|b \right)$$

这也比较直观，从 b c 传递给 a 的信息，来自于从 c 传递给 a 的信息和 a b 已知 c 的情况下，b 给 a 传递的信息。

平均互信息量的三个视角

从信息传递的角度看，可以分别从信源 X 的角度、信宿 Y 的调度和通信系统整体的角度，看待平均互信息量（传输的信息量）和信源熵（信源传输信息的能力）。

从信源 X：

$$I\left( Y;X \right) =H\left( Y \right) -H\left( Y|X \right)$$

这表示 X 发送信息后，从 X 观察 Y，Y 剩下的不确定度，也就是信息熵。

从信宿 Y：

$$I\left( X;Y \right) =H\left( X \right) -H\left( X|Y \right)$$

这表示 Y 接收信息后，从 Y 观察 X，X 剩下的不确定度，也就是信息熵。

从通信系统：

$$I\left( X;Y \right) =H\left( X \right)+ H\left( Y \right)-H\left( XY \right)$$

这表示原本传递信息之前，X 和 Y 是独立的，提供的信息熵为 $H\left( X \right)+ H\left( Y \right)$。但是当 X 和 Y 通信后，X Y 作为整体所提供的信息熵就变成了 $H\left( XY \right)$，二者之差就是传递的信息量。

信源熵互信息量的关系

下面的图中，$I(X;Y)$ 表示 X Y 重叠部分，$H(XY)$ 表示两个圆的组合，$H(X/Y)$ 表示圆 X 挖去了圆 Y 的部分。

单符号离散信道容量

仍然假设输入$X\in { a_1,a_2,\cdots a_n } $，输出 $Y \in\{b_1, b_2, \cdots b_m\}$，那么信息从 X 传递到 Y 的转移概率矩阵，也叫做信道矩阵如下：

$$\left[\begin{array}{c} p\left(b_1 / a_1\right), p\left(b_2 / a_1\right), \cdots, p\left(b_m / a_1\right) \\ p\left(b_1 / a_2\right), p\left(b_2 / a_2\right), \cdots, p\left(b_m / a_2\right) \\ \cdots \cdots \\ p\left(b_1 / a_n\right), p\left(b_2 / a_n\right), \cdots, p\left(b_m / a_n\right) \end{array}\right]$$

信道容量通过调整 $p(a_i)$的概率分布，实现 X 和 Y 最大的互信息量，也就是最大的可以承载的能力。

$$\begin{aligned} C & =\max _{p\left(a_i\right)} I(X ; Y) \\ & =\max _{p\left(a_i\right)}[H(X)-H(X / Y)]=\max _{p\left(a_i\right)}[H(Y)-H(Y / X)] \end{aligned}$$

一般的信道容量是比较复杂的，只需要掌握特殊的即可。很多时候入门信息论，都是定性分析。优化的变量，都是 X 的符号的概率，而不是 Y 的概率。

无噪声 X 和 Y 一对一：

那么转移概率矩阵就是每行一个 1，而且每列一个 1，那么 $H(X|Y)=H(Y|X)=0$

$$C=\max H(X)=\log n$$

无噪声 X 和 Y 一对多：

信道矩阵就是每行若干个概率，但是每一列只有一个不为 0

$$\left[ \begin{matrix} p\left( b_1/a_1 \right)& p\left( b_2/a_1 \right)& p\left( b_3/a_1 \right)& 0& 0& 0& 0& 0\\ 0& 0& 0& p\left( \left. b_4/a_2 \right) \right.& p\left( b_5/a_2 \right)& p\left( b_6/a_2 \right)& 0& 0\\ 0& 0& 0& 0& 0& 0& p\left( b_7/a_3 \right)& p\left( b_8/a_3 \right)\\ \end{matrix} \right]$$

那么 $H(X|Y)=0$ 但是 $H(Y|X)\ne 0$，而且 $H(X)<H(Y)$

$$C=\max H(X)=\log n$$

无噪声多对一：

类似于 $a_1 \rightarrow b_1$ $a_2 \rightarrow b_1$，所以信道矩阵如下：

$$\left[\begin{array}{lll} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$$

这样就有 $H(Y|X)=0$，所以

$$C=\max H(Y)=\log m$$

强对称：

对于信道 ${ X,, P\left( Y|X \right) ,,Y } $ ，输入和输出的符号种类数量相同，而且每个符号传递对应传递的概率为 $1-p$，其他传递错误的可能性平分。每一行和每一列都是 1。也就是如下

$$\begin{gather*} X\in \left\{ a_1,a_2,.......a_n \right\} ,\quad Y\in \left\{ b_1,b_2,......b_m \right\} \\ \left[ \begin{matrix} 1-p& \frac{p}{n-1}& .....& \frac{p}{n-1}\\ \frac{p}{n-1}& 1-p& ....& \frac{p}{n-1}\\ \frac{p}{n-1}& \frac{p}{n-1}& ....& 1-p\\ \end{matrix} \right] _{n\times n} \end{gather*}$$

那么很特殊的性质就是 $H(Y|X)$ 是常数，因为每一行信源熵都相等，所以

$$\sum_{j=1}^n{p\left( b_j/a_i \right) \log p\left( b_j/a_i \right)}=(1-p)\log\mathrm{(}1-p)+\left( \frac{p}{n-1}\log \frac{p}{n-1} \right) (n-1)$$

令这个常数为 $H_{ni}$，就得到了下面的结论

$$\begin{aligned} H(Y/X)&=-\sum_{i=1}^n{\sum_{j=1}^n{p}}\left( a_i \right) p\left( b_j/a_i \right) \log p\left( b_j/a_i \right) =-\sum_{i=1}^n{p}\left( a_i \right) \sum_{j=1}^n{p}\left( b_j/a_i \right) \log p\left( b_j/a_i \right)\\ &=-\sum_{i=1}^n{p}\left( a_i \right) H_{ni}=H_{ni}\\ \end{aligned}$$

$H_{ni}$ 随着 p 变化的函数图像如下：

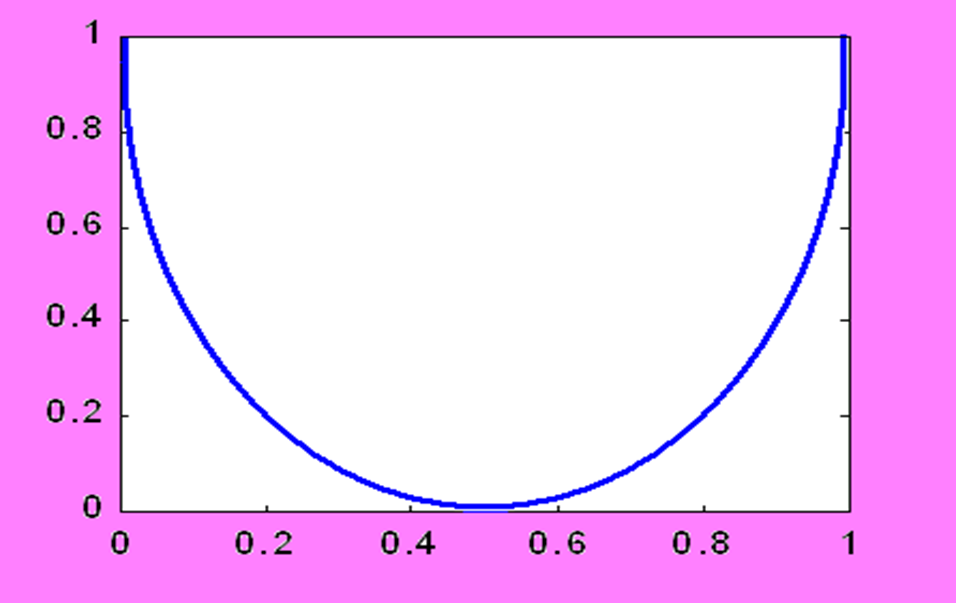
最后，当整个信道矩阵都是 $\frac{1}{n}$ 的时候，取到最大。具体过程忽略

$$\begin{align*} &C=\max_{p\left( a_i \right)} I(X;Y)=\max_{p\left( a_i \right)} [H(Y)-H(Y/X)] \\ &=\max_{p\left( a_i \right)} \left[ H(Y)-H_n \right] =\log n-H_{ni} \end{align*}$$

对称：

对称信道和强对称信道有类似之处，但是条件更加宽松，只需要每一列是同一个集合的排列，每一行也是同一个集合的排列，不再需要 $a_i \rightarrow b_i$，也不需要错误映射的可能性平分。

这样就会出现有趣的性质，因为每一行的和为 1，假设是 ${q_1,q_2,\cdots,q_n}$ 这 n 个可以重复的元素，那么每一列都包括了其中一个元素，那么如果 m<n，那么列的元素的集合一定是行元素集合的子集。m>n 时，也有对应的结论。

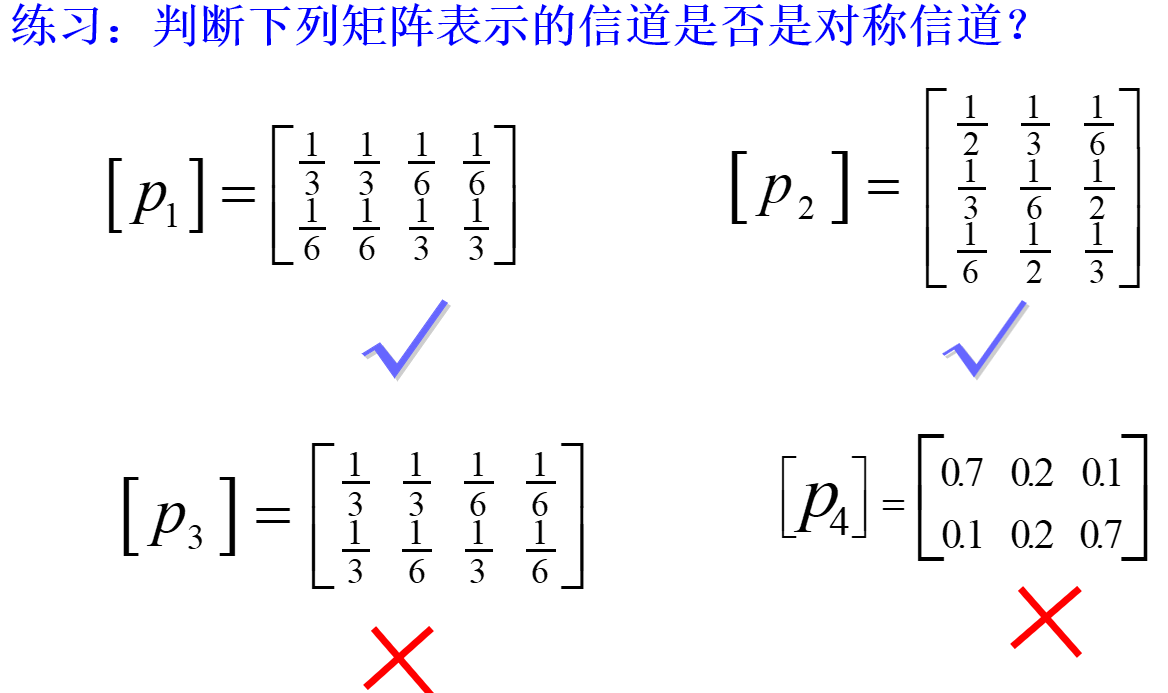对于这样的信道矩阵，可以明显知道，每一行的信息量是相等的，也即

$$\begin{aligned} &H(Y/X)=-\sum_{i=1}{\sum_{j=1}{p}}\left( a_i \right) p\left( b_j/a_i \right) \log p\left( b_j/a_i \right)\\ &=-\sum_{i=1}^n{p}\left( a_i \right) \left[ \sum_{j=1}^m{p}\left( b_j/a_i \right) \log p\left( b_j/a_i \right) \right]\\ &=H_{mi}\\ \end{aligned}$$

可以发现，和强对称矩阵不一样了，虽然取等条件也是X每个符号等概率，但是最大值是由 Y 的符号个数决定了。

$$C=\max_{p\left( a_i \right)} \left[ H(Y)-H_{mi} \right] =\log m-H_{mi}$$

准对称矩阵：

每一行都是同一个集合的排列，列不是。但是列可以通过分组，把原来的 n*m 的矩阵，分组成 $n*m_1, n*m_2,\cdots,n*m_s$ 这个 s 个矩阵。

(待续)

（不写笔记了，这门课很多概念就是没有搞清楚，课程要求也是会背公式，计算就可以了。我去理解原理反而有害分数，而且非常费力。）